Transcritical Bifurcation of a Nonlinear Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
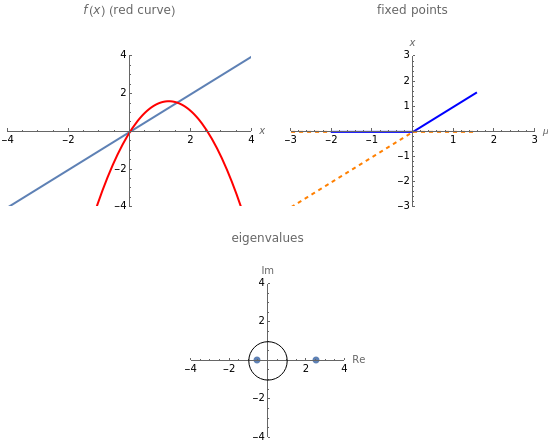
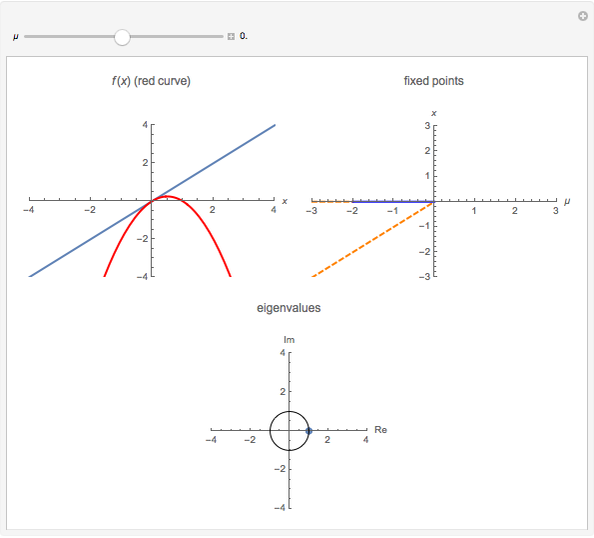
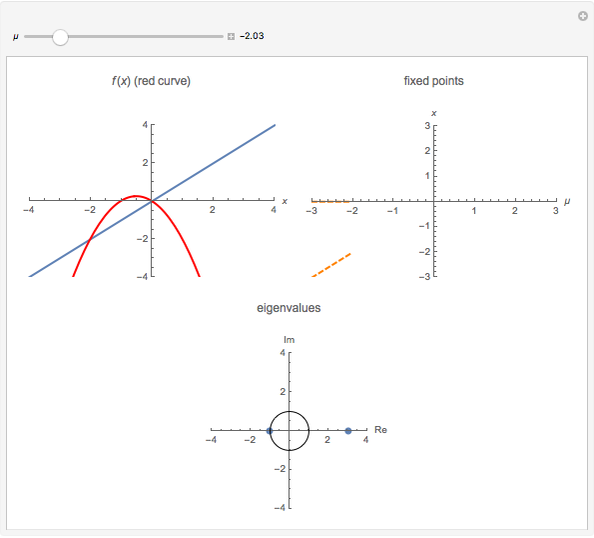
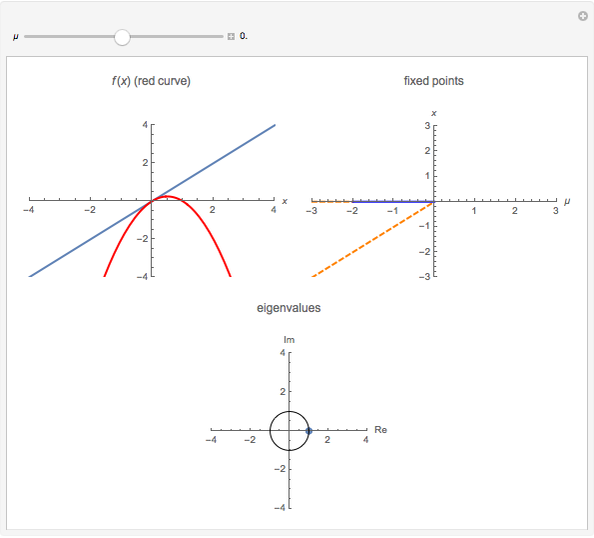
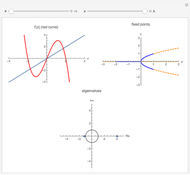
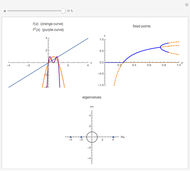
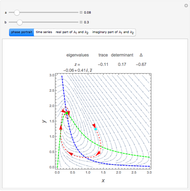
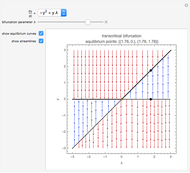
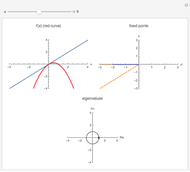
A transcritical bifurcation of the function 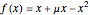 occurs when increasing the parameter
occurs when increasing the parameter  causes the graph of
causes the graph of 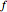 to intersect the line
to intersect the line  . See Example 2.30 in [1]. Intersections with the line correspond to fixed points for the map, which are plotted in the figure at the top right; solid lines represent stable fixed points and dashed lines represent unstable fixed points. Eigenvalues inside the unit circle correspond to stable fixed points; eigenvalues outside to unstable fixed points. The eigenvalues for the fixed points at particular values of
. See Example 2.30 in [1]. Intersections with the line correspond to fixed points for the map, which are plotted in the figure at the top right; solid lines represent stable fixed points and dashed lines represent unstable fixed points. Eigenvalues inside the unit circle correspond to stable fixed points; eigenvalues outside to unstable fixed points. The eigenvalues for the fixed points at particular values of  are shown at the bottom of the figure.
are shown at the bottom of the figure.
Contributed by: Edmon Perkins (January 2019)
After work by: Ali Nayfeh and Balakumar Balachandran
Open content licensed under CC BY-NC-SA
Details
Reference
[1] A. H. Nayfeh and B. Balachandran, Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods, New York: Wiley, 1995.
Snapshots
Permanent Citation