Bifurcation Diagrams with Flow Fields

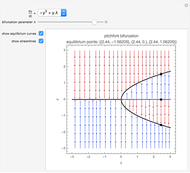
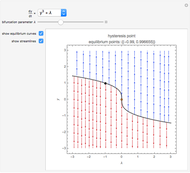
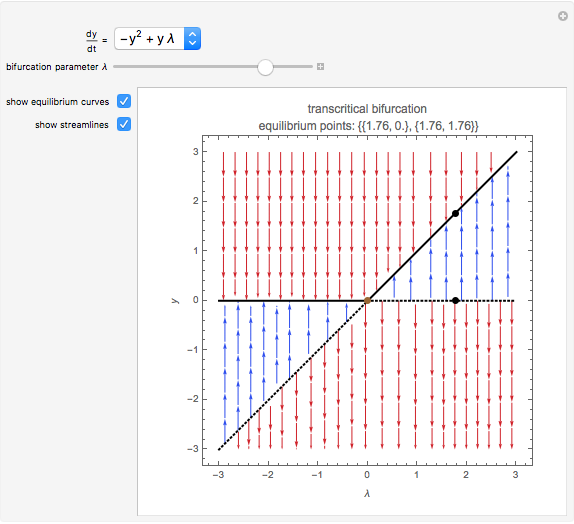
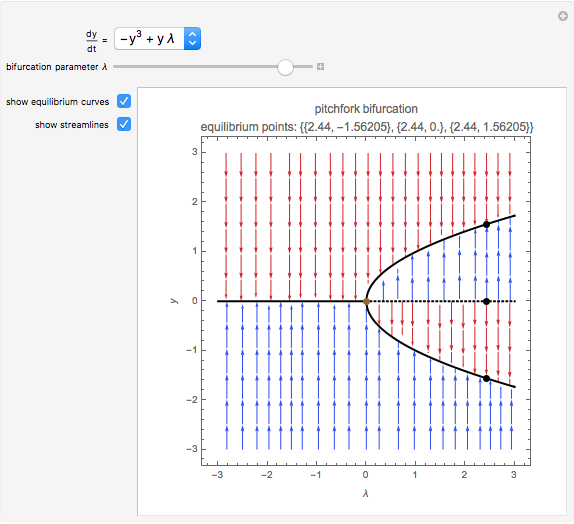
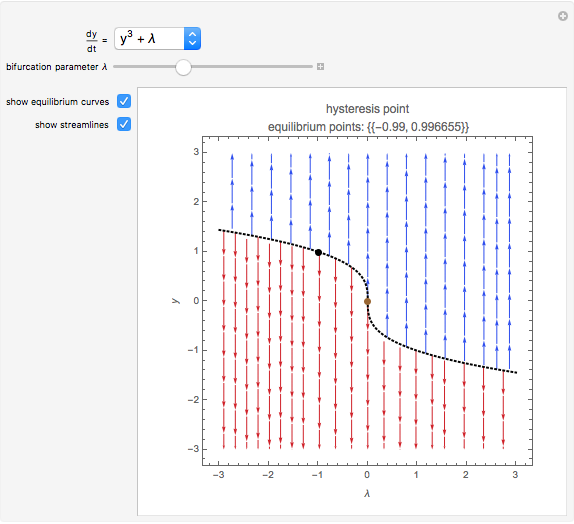
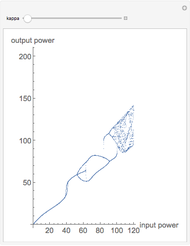
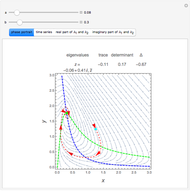
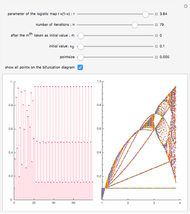
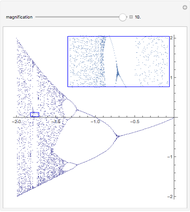
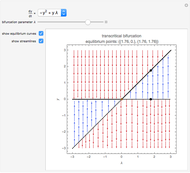
Bifurcations indicate qualitative changes in a system's behavior. For a dynamical system , bifurcation points are those equilibrium points at which the Jacobian 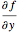is singular. This Demonstration shows the bifurcation diagrams of several normal form bifurcations in one dimension. The bifurcation point, equilibrium points, and the flow of the vector field are visualized. The bifurcation is shown as a brown point. Solid black lines indicate stable equilibrium branches and dashed black lines indicate unstable ones.