Hopf Bifurcation in the Brusselator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
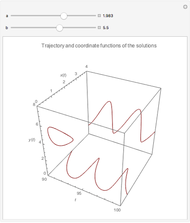
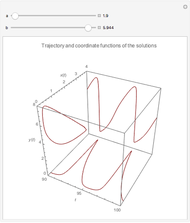
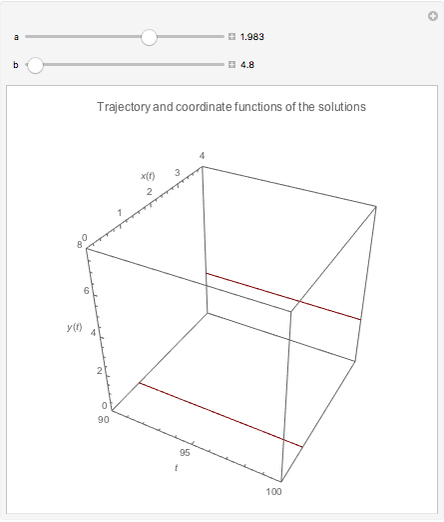
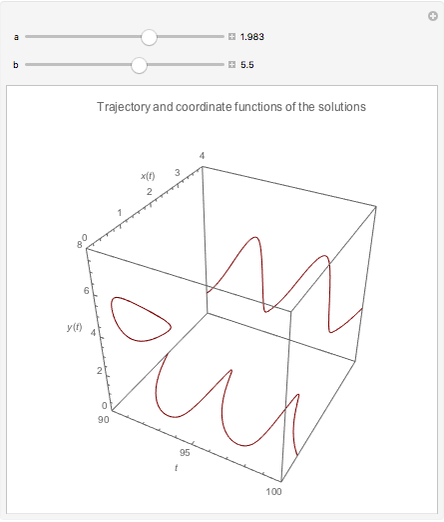
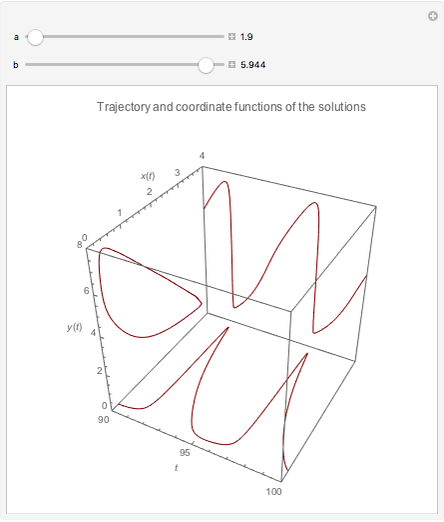
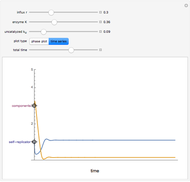
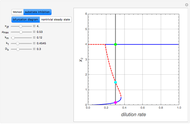
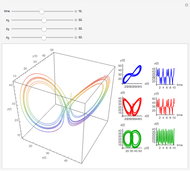
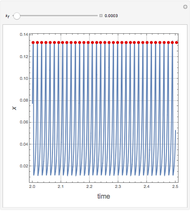
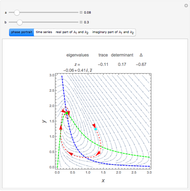
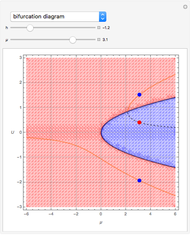
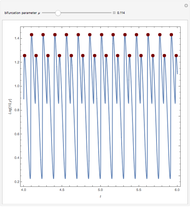
The Brusselator is a model for chemical oscillation with a limit cycle. The emergence of the limit cycle can be proven by the Andronov–Hopf bifurcation theorem.
Contributed by: Judit Várdai and János Tóth (March 2011)
After work by: I. Prigogine and R. Lefever
Open content licensed under CC BY-NC-SA
Snapshots
Details
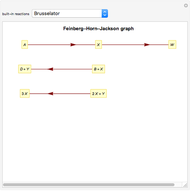
The dynamics and chemistry of oscillating reactions has been the subject of study only for the last 50 years, starting with the work of Belousov. The mechanism for the Brusselator is given by  . The two species of interest are
. The two species of interest are  and
and  , the autocatalytic species. The differential equations given in dimensionless form for these species are
, the autocatalytic species. The differential equations given in dimensionless form for these species are  and
and  . For this analysis all rate constants except those of the second step are assumed to equal 1 and the reactants
. For this analysis all rate constants except those of the second step are assumed to equal 1 and the reactants  and
and  are assumed to be in large enough excess so that their concentrations do not change with time. Both the parameters
are assumed to be in large enough excess so that their concentrations do not change with time. Both the parameters  and
and  are changed in the Demonstration, and as a result concentration-time curves and trajectories (selectivity curves in chemical terms) are shown.
are changed in the Demonstration, and as a result concentration-time curves and trajectories (selectivity curves in chemical terms) are shown.
Reference: I. Prigogine and R. Lefever, "Symmetry Breaking Instabilities in Dissipative Systems II," Journal of Chemical Physics, 48, 1968 pp. 1695–1700.
Permanent Citation
"Hopf Bifurcation in the Brusselator"
http://demonstrations.wolfram.com/HopfBifurcationInTheBrusselator/
Wolfram Demonstrations Project
Published: March 7 2011