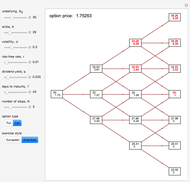
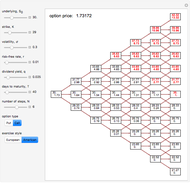
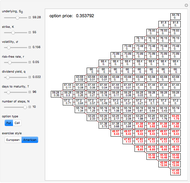
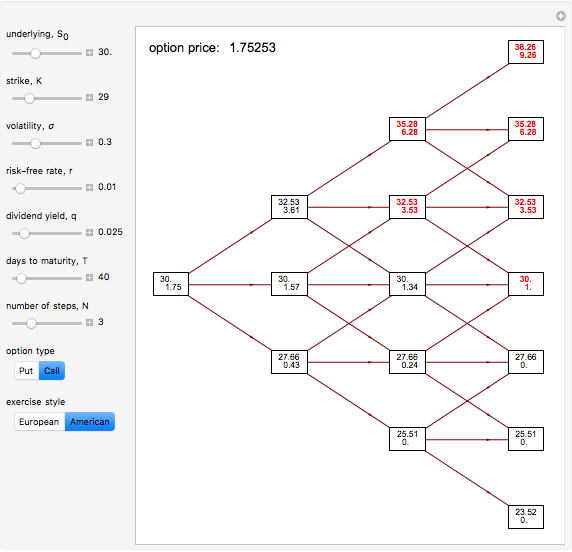
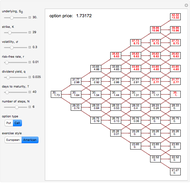
Trinomial Tree Option Pricing Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
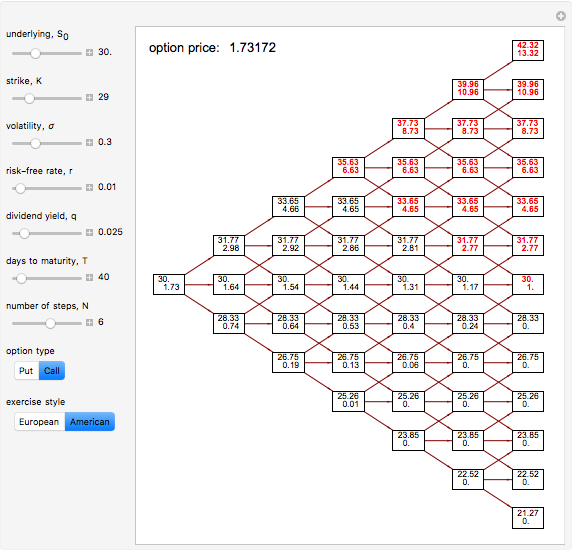
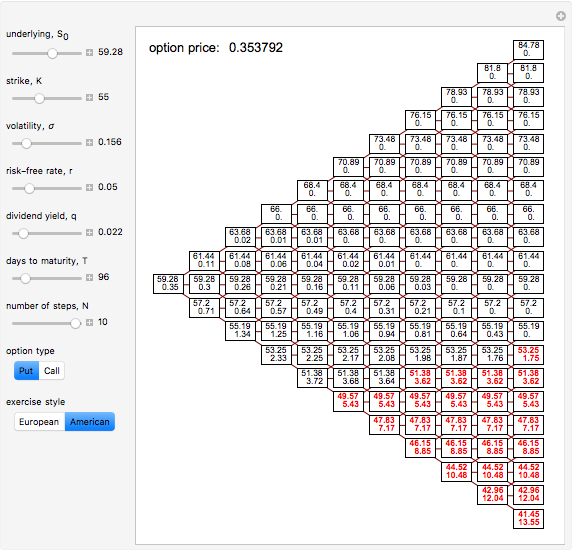
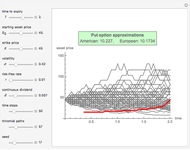
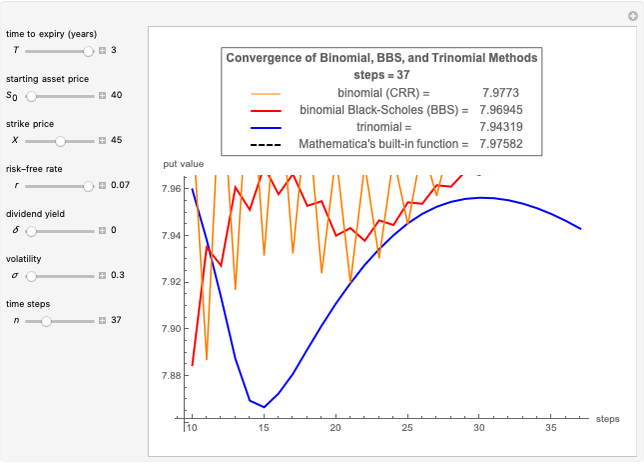
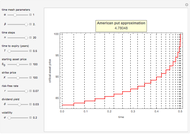
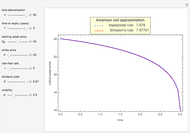
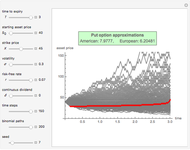
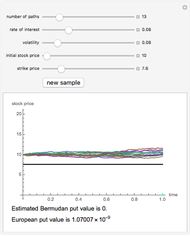
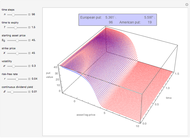
This Demonstration illustrates the application of the recombining trinomial tree method to approximate the value of the European- or American-type call/put option, assuming constant volatility and risk-free interest rate. A call/put option gives its owner the right but not the obligation to purchase/sell the underlying asset (e.g., equity share) at a price agreed in advance—the strike price. The European-type call/put option may be exercised only on the expiration date of the option. In contrast, the American-type call/put option may be exercised at any time between its inception and expiration. Therefore, the American-type call/put option offers its owner more optionality relative to the European-type option. Hence, the price of the American-type call/put option is at least the same as the European-type call/put option, or more.
[more]
Contributed by: Darius Kirevicius (December 2014)
Open content licensed under CC BY-NC-SA
Details
The Demonstration illustrates application of the recombining trinomial tree model to approximate the value of the European- and American-type call/put options. The recombining trinomial tree is generated by allowing only three things to happen to the price of the underlying asset: increase, decrease, or remain unchained, one unit of time later (e.g., one tick, day, week, etc.). Specifically, the underlying asset price is allowed to: (1) increase by the factor 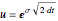 ; (2) decrease by the factor
; (2) decrease by the factor 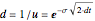 ; or (3) remain unchanged, hence scaled by the factor
; or (3) remain unchanged, hence scaled by the factor 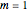 , where
, where  is the annualized volatility of the underlying asset and
is the annualized volatility of the underlying asset and 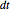 is the unit of time between successive tree nodes. Each of the three possible outcomes
is the unit of time between successive tree nodes. Each of the three possible outcomes  ,
,  , and
, and 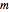 is assigned its risk-neutral probabilities
is assigned its risk-neutral probabilities 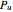 ,
, 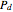 , and
, and 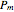 :
:
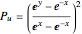 ,
,
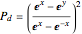 ,
,
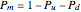 ,
,
where 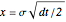 ,
, 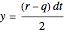 ,
,  is the risk-free rate (annualized),
is the risk-free rate (annualized),  is the dividend yield of the underlying asset (annualized), and
is the dividend yield of the underlying asset (annualized), and  and
and 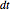 are as defined above. Further, to ensure that probabilities
are as defined above. Further, to ensure that probabilities 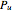 ,
, 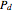 , and
, and 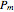 are in the interval of (0, 1) and their sum is equal to 1, the following condition must hold:
are in the interval of (0, 1) and their sum is equal to 1, the following condition must hold: 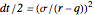 .
.
References
[1] J. Cox, S. Ross, and M. Rubinstein, "Option Pricing: A Simplified Approach," Journal of Financial Economics, 7(3), 1979 pp. 229–263. doi:10.1016/0304-405X(79)90015-1.
[2] J. C. Hull, Options, Futures, and Other Derivatives, 8th ed., Boston: Prentice Hall, 2012.
[3] N. N. Taleb, Dynamic Hedging: Managing Vanilla and Exotic Options, New York: John Wiley & Sons, Inc., 1997.
Snapshots
Permanent Citation