Kim's Method for Pricing American Options

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
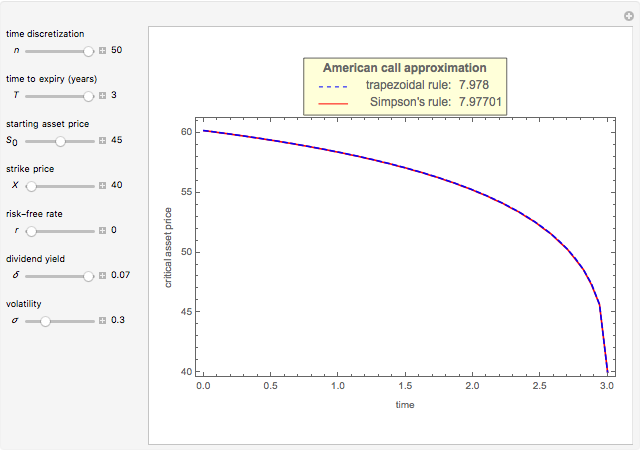
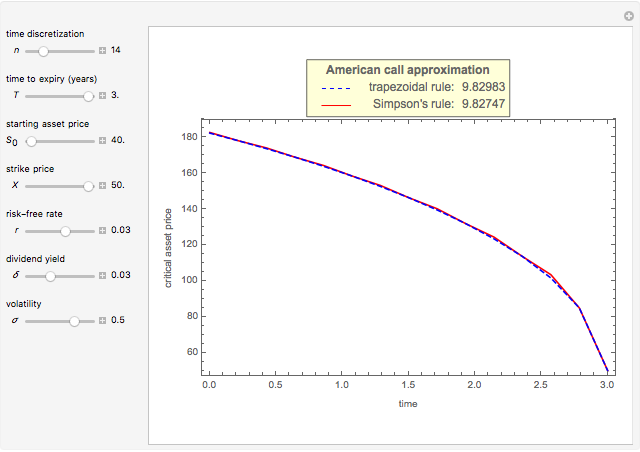
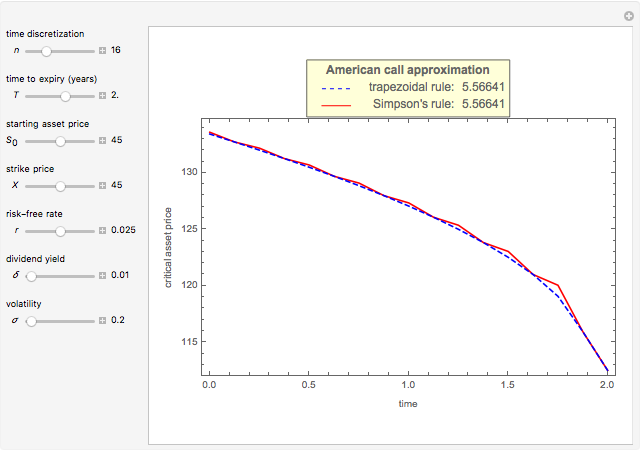
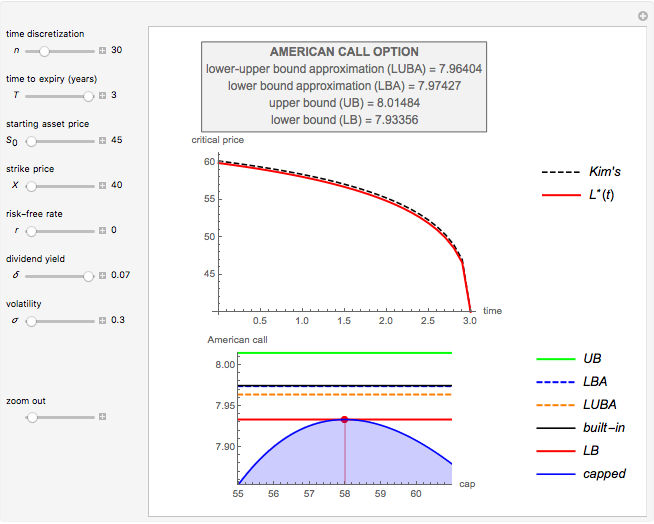
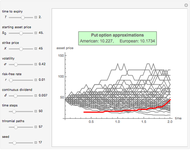
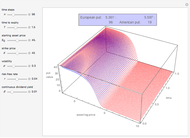
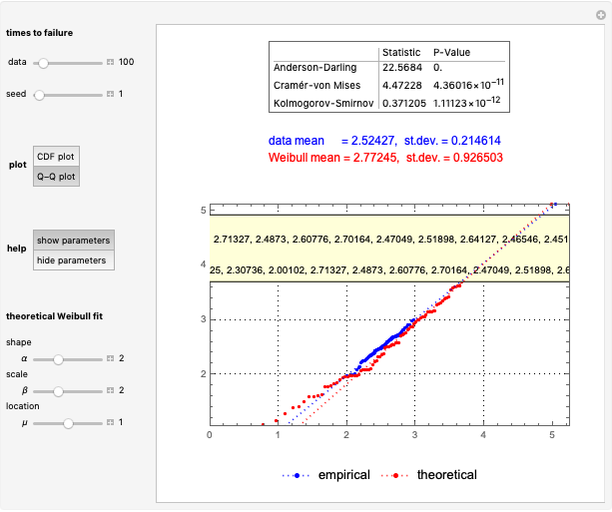
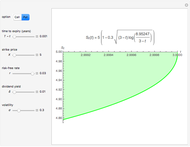
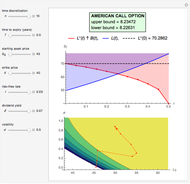
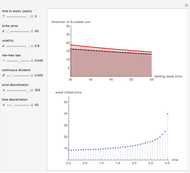
This Demonstration shows Kim's method [1] for pricing American options. A European financial option is an instrument that allows its holder the right to buy or sell an equity at a future maturity date for a fixed price called the "strike price." An American option allows its holder to exercise the contract at any time up to the maturity date, and because of this it is worth more than the European option, by an amount called the "early exercise premium." For the American call's holder, the early exercise becomes optimal when the underlying asset price exceeds a critical boundary  , above which the intrinsic value of the option becomes greater than its holding value.
, above which the intrinsic value of the option becomes greater than its holding value.
Contributed by: Michail Bozoudis (May 2016)
Suggested by: Michail Boutsikas
Open content licensed under CC BY-NC-SA
Snapshots
Details
In this detailed description, the symbols have the following meanings:  : current time;
: current time;  : maturity date;
: maturity date;  : stock price at time
: stock price at time  ;
;  : strike price;
: strike price;  : stock dividend yield;
: stock dividend yield;  : risk-free interest rate;
: risk-free interest rate;  : stock volatility;
: stock volatility; 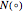 : the cumulative distribution function of the standard normal distribution;
: the cumulative distribution function of the standard normal distribution; 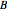 : the moving free boundary;
: the moving free boundary; 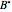 : the optimal boundary.
: the optimal boundary.
Consider the class of contracts consisting of a European call option and a sure flow of payments that are paid at the rate
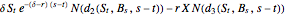 for
for 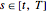 ,
,
where
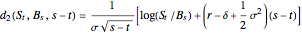 ,
,
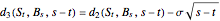 ,
,
and 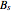 is a non-negative continuous function of time. Each member of the class of contracts is parametrized by
is a non-negative continuous function of time. Each member of the class of contracts is parametrized by 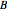 . The value of the contract at time
. The value of the contract at time  is
is
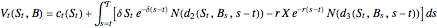 ,
,
where 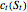 denotes the value at time
denotes the value at time  of a European call option on
of a European call option on 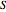 with strike price
with strike price 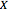 and maturity
and maturity  . The optimal exercise boundary
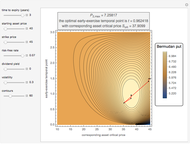
. The optimal exercise boundary 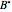 for the American call option is obtained by solving the "value matching condition":
for the American call option is obtained by solving the "value matching condition":
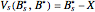 , for
, for  for all
for all 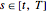 .
.
The value of the American call option 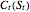 is then given by
is then given by  .
.
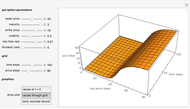
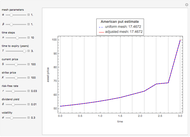
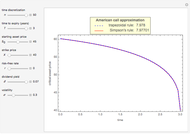
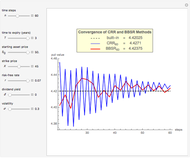
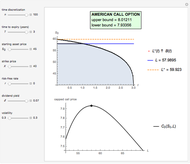
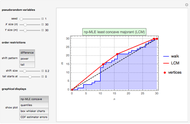
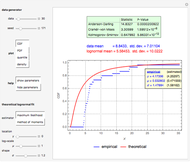
Subject to the "value matching condition," the critical asset price at time  can be numerically approximated by a computationally intensive recursive procedure. This method requires solving
can be numerically approximated by a computationally intensive recursive procedure. This method requires solving  integral equations, where
integral equations, where  is the number of time steps. Each time the integral equation is solved, either the trapezoidal rule (Wolfram MathWorld) or Simpson's rule (Wolfram MathWorld) is employed to approximate the integral.
is the number of time steps. Each time the integral equation is solved, either the trapezoidal rule (Wolfram MathWorld) or Simpson's rule (Wolfram MathWorld) is employed to approximate the integral.
References
[1] I. J. Kim, “The Analytic Valuation of American Options,” Review of Financial Studies, 3(4), 1990 pp. 547–572. www.jstor.org/stable/2962115.
[2] M. Broadie and J. Detemple, "American Option Valuation: New Bounds, Approximations, and a Comparison of Existing Methods," The Review of Financial Studies, 9(4), 1996 pp. 1211–1250. doi:10.1093/rfs/9.4.1211.
Permanent Citation