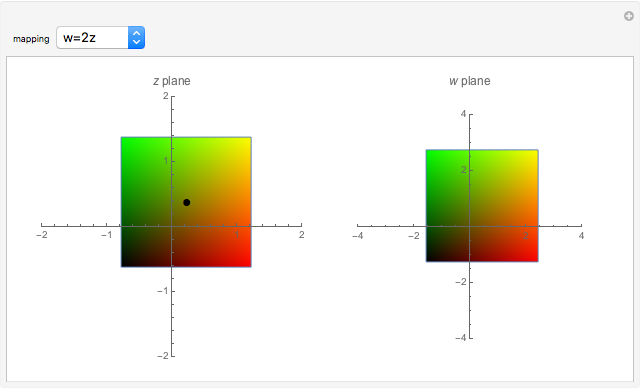
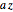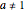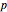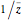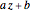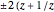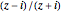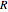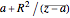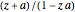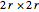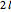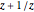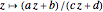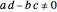• scaling and rotating with respect to the origin: 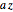
• spiraling:  , for
, for 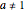 and varying
and varying 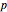 ; depending on the values, the spiral goes in or out
; depending on the values, the spiral goes in or out
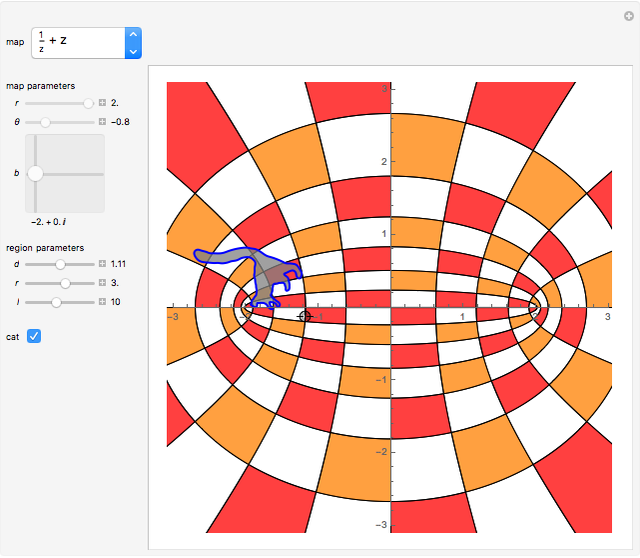
• inversion in the unit circle: 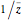 ; points on the unit circle are fixed, the interior of the unit circle is mapped to the exterior and vice versa
; points on the unit circle are fixed, the interior of the unit circle is mapped to the exterior and vice versa
• scaling and rotating with respect to the center point  :
: 
• scaling and rotating with respect to the origin, then translating: 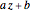
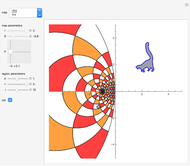
• Joukowski map:  ; points on the unit circle are mapped to the line between the two points
; points on the unit circle are mapped to the line between the two points 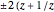 ). Circles are mapped to ellipses.
). Circles are mapped to ellipses.
• Cayley map: 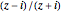 ; maps the upper complex half-plane to the unit disk
; maps the upper complex half-plane to the unit disk
• inversion in a circle of radius 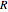 whose center is
whose center is  :
: 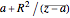 ; defined for any circle in the plane
; defined for any circle in the plane
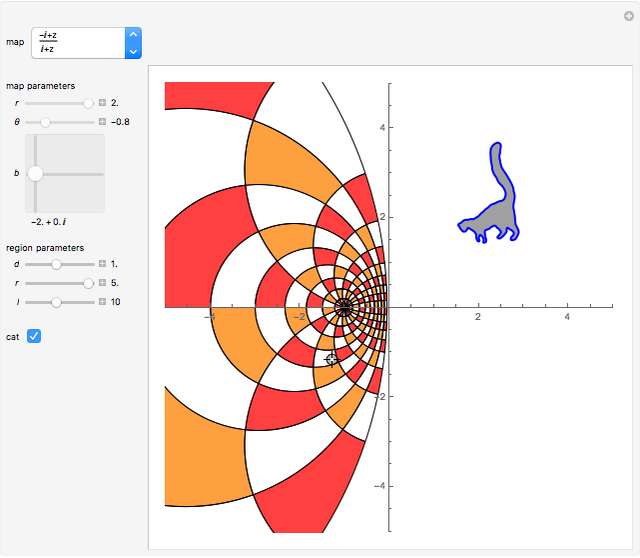
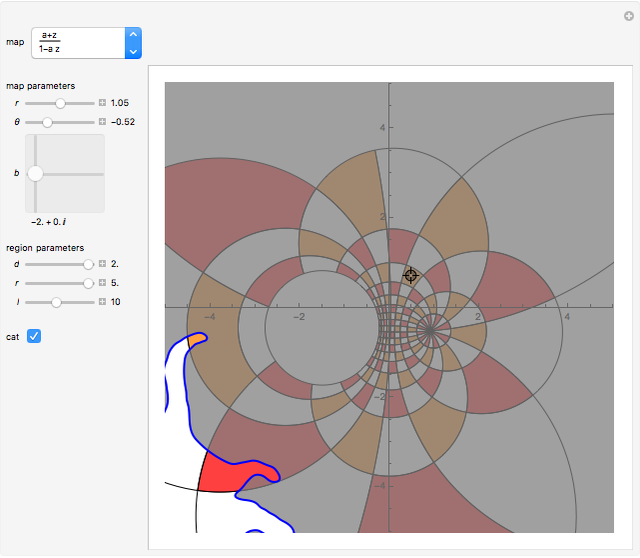
• a particular Möbius transformation: 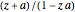 ; it preserves angles locally and maps generalized circles to generalized circles
; it preserves angles locally and maps generalized circles to generalized circles
The mappings are evaluated over a  domain and plotted on a region of dimensions
domain and plotted on a region of dimensions 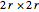 , with
, with 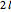 lines.
lines.
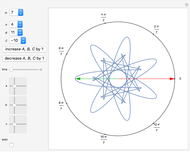
Compositions of these transformations give more elaborate transformations, for example, the spiraling transformation can be composed with the transformation 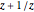 to give a double spiral.
to give a double spiral.
A Möbius transformation has the form 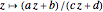 , where
, where 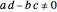 . A Möbius transformation can be decomposed into a composition of translations, reflections, rotations, and inversions. The composition of two Möbius transformations is another Möbius transformation. Mastering these compositions with some particular cases of Möbius transformations leads to the construction of Schottky groups [1].
. A Möbius transformation can be decomposed into a composition of translations, reflections, rotations, and inversions. The composition of two Möbius transformations is another Möbius transformation. Mastering these compositions with some particular cases of Möbius transformations leads to the construction of Schottky groups [1].
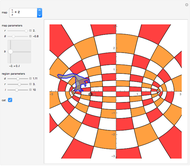
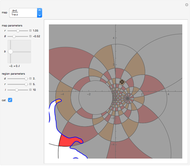
The locator is the position of the pre-image of the cat. Drag the locator to see where the map puts the cat, which is not always clear. You can even drag the locator outside the mesh. The cat helps to see if a mesh is rotated or reflected. Try to move the cat along a desired path. Sometimes it is odd to see the effect of the mapping on the cat and sometimes the cat looks very big.
[less]

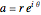 and
and  ):
):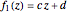 ,
, 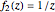 ,
, 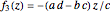 ,
, 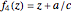 ,
,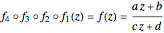 .
.