Variational Principle for Quantum Particle in a Box

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
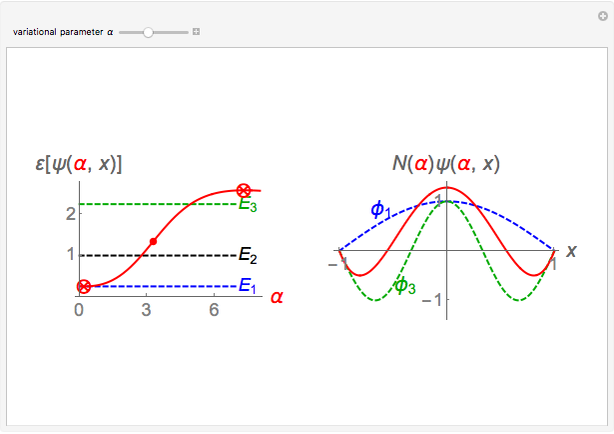
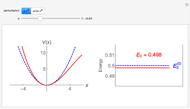
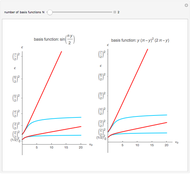
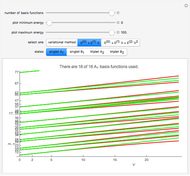
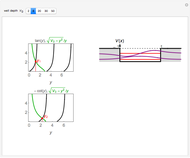
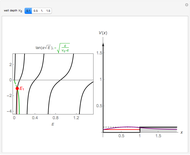
This Demonstration shows the variational principle applied to the quantum particle-in-a-box problem. The Hamiltonian describing the particle is  , and the eigenfunctions and eigenvalues are given by
, and the eigenfunctions and eigenvalues are given by  and
and  , respectively. If
, respectively. If  is a trial wavefunction that depends on the variational parameter
is a trial wavefunction that depends on the variational parameter  , then minimizing the energy functional
, then minimizing the energy functional  with respect to
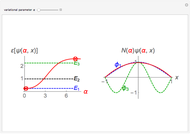
with respect to  leads to an estimate for the energy. In this example, the values of
leads to an estimate for the energy. In this example, the values of  that minimize
that minimize  are
are  and
and  ,
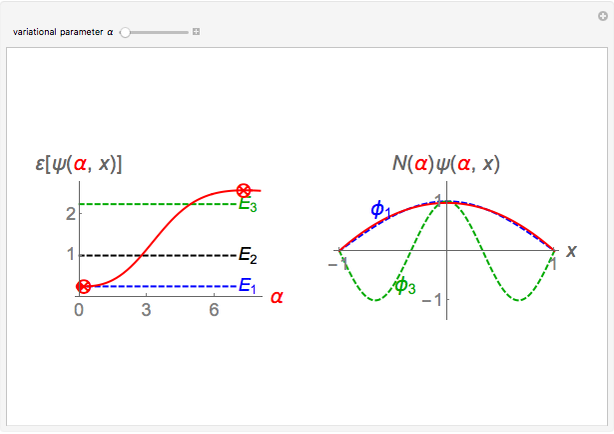
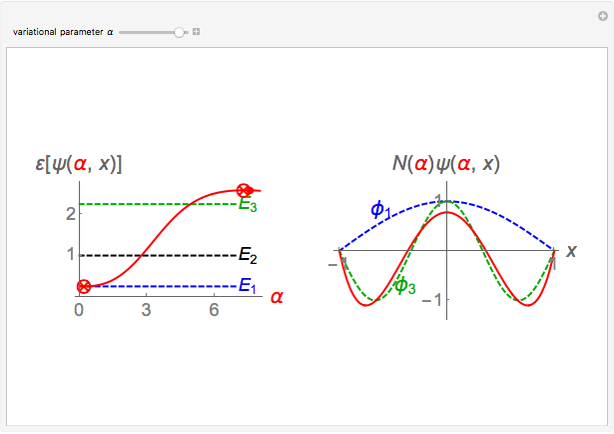
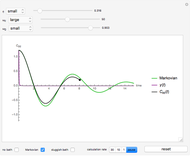
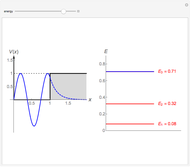
,  . The left panel shows the energy estimate and the three lowest eigenenergies, where the red
. The left panel shows the energy estimate and the three lowest eigenenergies, where the red  are located at the
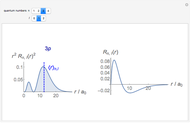
are located at the  , and the right graphic shows the normalized trial wavefunction for the ground and second excited states, which are the lowest even functions with respect to the central point.
, and the right graphic shows the normalized trial wavefunction for the ground and second excited states, which are the lowest even functions with respect to the central point.
Contributed by: Porscha McRobbie and Eitan Geva (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Variational Principle for Quantum Particle in a Box"
http://demonstrations.wolfram.com/VariationalPrincipleForQuantumParticleInABox/
Wolfram Demonstrations Project
Published: March 7 2011