What Does "Inside" Mean?

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
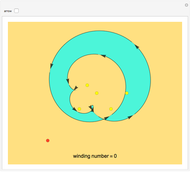
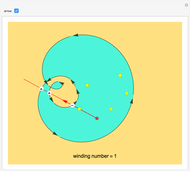
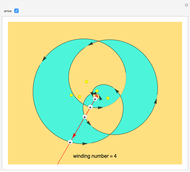
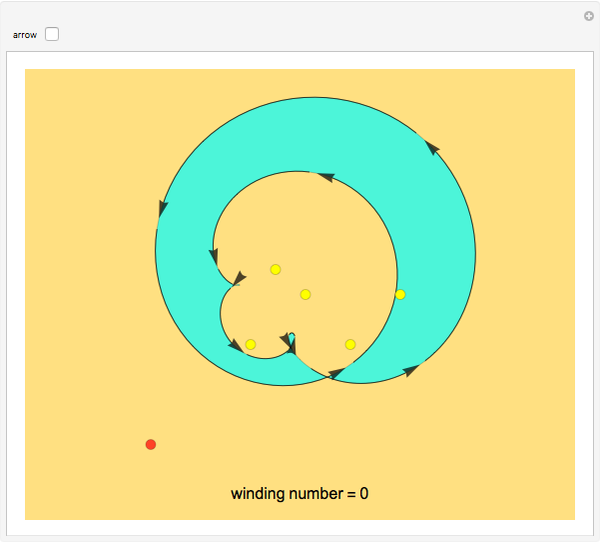
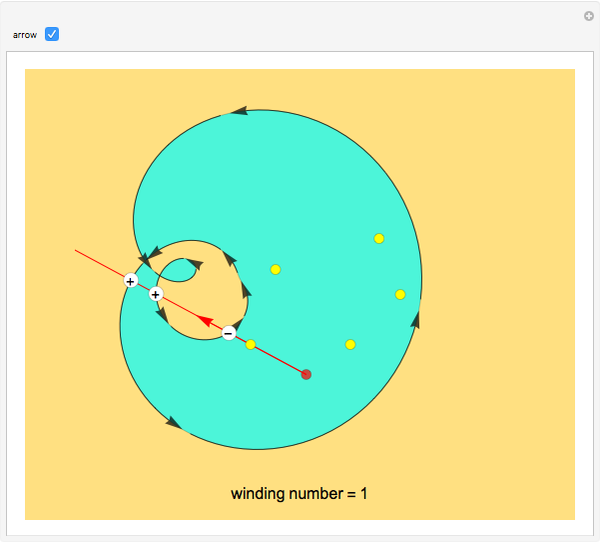
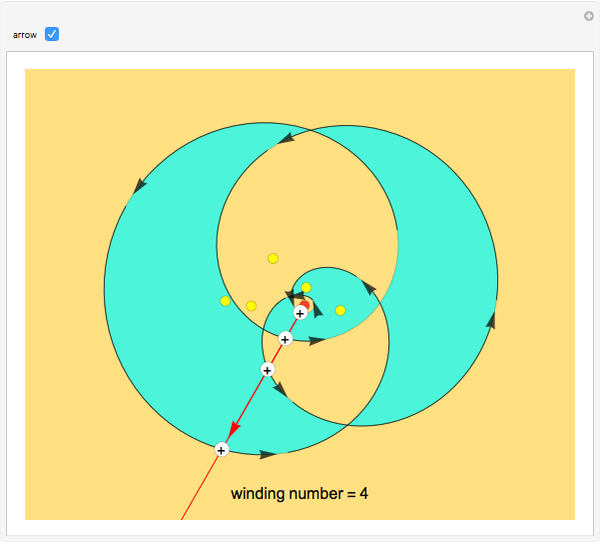
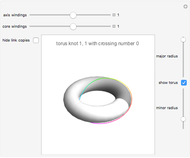
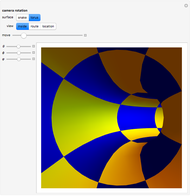
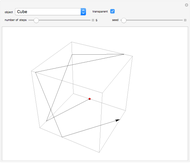
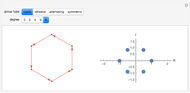
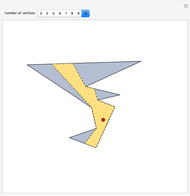
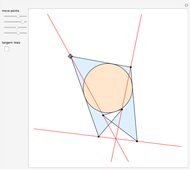
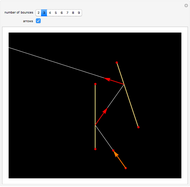
Consider a closed directed curve (or loop) in the plane. If this loop is simple, that is, it does not intersect itself, then however complicated it might be, it will divide the plane into two sets: an inside and an outside. In the case of a non-simple loop, like the curve shown, it is no longer obvious which points are to be considered inside the loop and which outside. The winding number concept clarifies that distinction and plays a crucial role in understanding multifunctions and complex integration.
[more]
Contributed by: Jaime Rangel-Mondragon (September 2018)
Open content licensed under CC BY-NC-SA
Details
Reference
[1] T. Needham, Visual Complex Analysis, New York: Oxford University Press, 1997.
Snapshots
Permanent Citation