Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

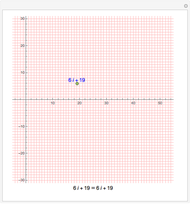
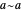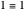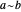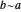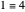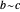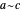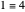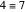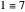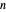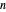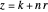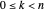Wheel of Congruence Classes of Integers Modulo n

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

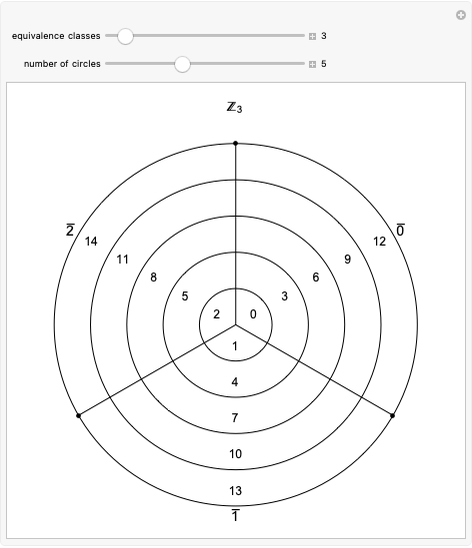
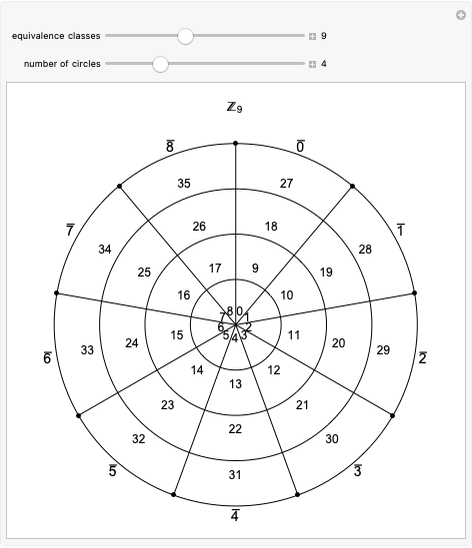
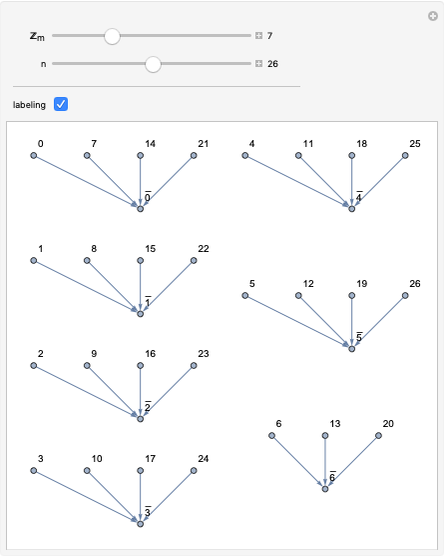
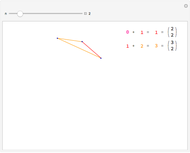
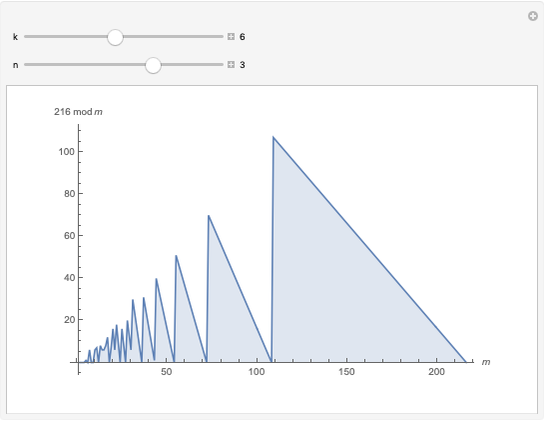
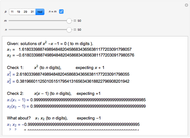
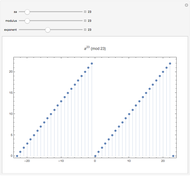
With respect to a relation 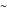, an equivalence class has three properties. Take as an example the integers modulo 3 with respect to congruence.

[more]

1. Reflexivity: . For example, modulo 3, .

2. Symmetry: implies . For example, modulo 3, and .

3. Transitivity: and implies . For example, modulo 3, , and .

The equivalence classes of the integers modulo can be represented as segments of a wheel, with the congruence class of each of the integers shown. Given a positive integer , each integer satisfies the formula , where . Here is the value of the equivalence class (shown over-lined), is the order of the additive group and is the segment, starting from 0 in the innermost circle.

[less]

Contributed by: Theo Williams (October 12)
Open content licensed under CC BY-NC-SA

Details

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send