Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Multiplication Tables for the Group of Integers Modulo n

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Given a positive integer , the set of positive integers coprime to satisfies the axioms for an Abelian group under the operation of multiplication modulo . For instance, and because . This Demonstration shows the array plot of the multiplication table modulo corresponding to .

Contributed by: Jaime Rangel-Mondragon (August 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The order of is given by Euler's totient function , implemented in Mathematica as EulerPhi[n], which for has values . is cyclic only if is , or , where is an odd prime and . The first few values for which is not cyclic are . Any generator in the cyclic case is called a primitive root modulo .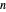

Reference

[1] Wikipedia. "Multiplicative Group of Integers Modulo n." (Jul 31, 2012) en.wikipedia.org/wiki/Multiplicative_group_of _integers _modulo _n.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send