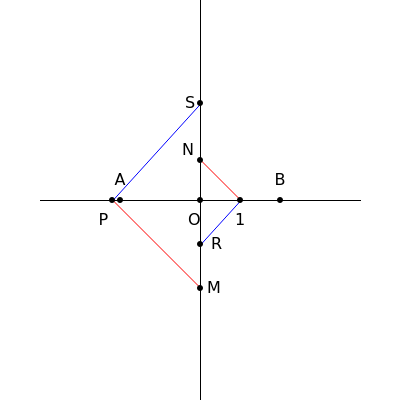
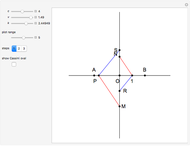
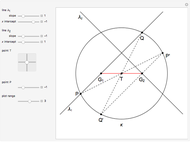
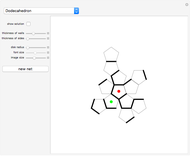
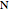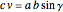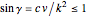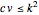33. Construct a Triangle Given Its Base, Altitude to the Base and Product of the Other Two Sides

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
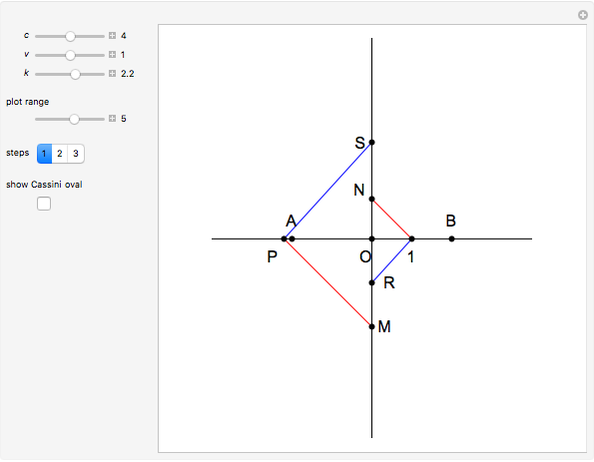
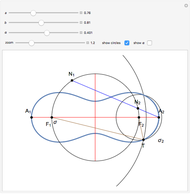
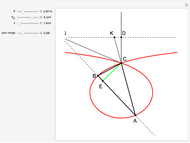
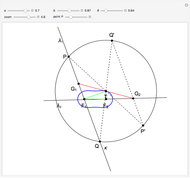
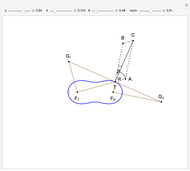
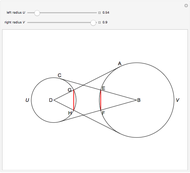
This Demonstration constructs a triangle 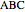 given the length
given the length  of the base
of the base  , the length
, the length  of the altitude from
of the altitude from  to
to 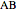 and the product
and the product 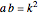 of the other two sides. Since the radius of the circumcircle
of the other two sides. Since the radius of the circumcircle 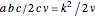 is a rational function of
is a rational function of  and
and  , we can construct it using similar triangles.
, we can construct it using similar triangles.
Contributed by: Izidor Hafner and Marko Razpet (October 2018)
Open content licensed under CC BY-NC-SA
Details
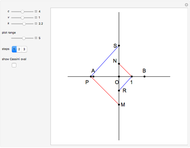
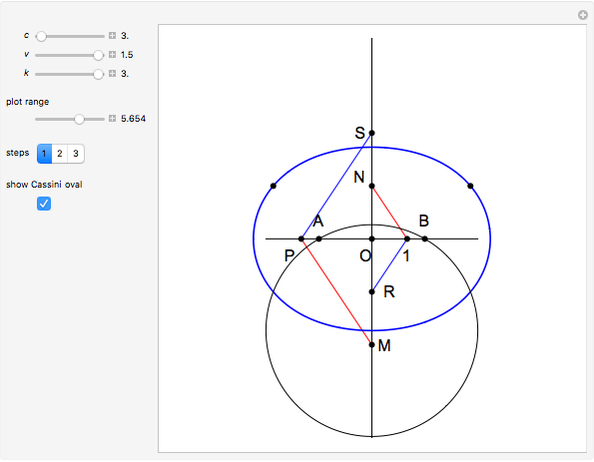
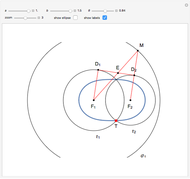
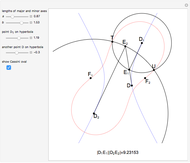
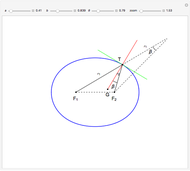
A Cassini oval (or Cassini ellipse) is a quartic curve such that if 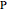 is on the curve, the product of its distances from two fixed points
is on the curve, the product of its distances from two fixed points  and
and 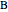 at a distance
at a distance  apart is a constant
apart is a constant  . Thus the original problem is equivalent to finding the intersections of the oval with a line parallel to the
. Thus the original problem is equivalent to finding the intersections of the oval with a line parallel to the  axis at distance
axis at distance  .
.
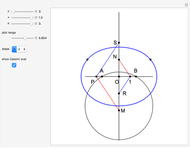
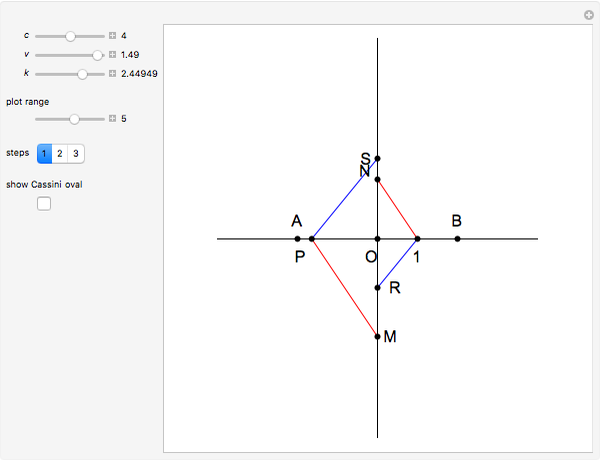
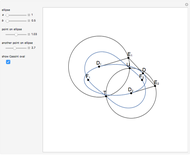
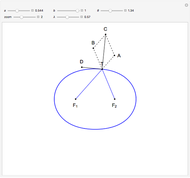
Keeping  and
and  fixed and changing
fixed and changing  , we get another construction of points on the Cassini oval.
, we get another construction of points on the Cassini oval.
Snapshots
Permanent Citation