Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Dissection Proof of Pythagoras's Theorem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

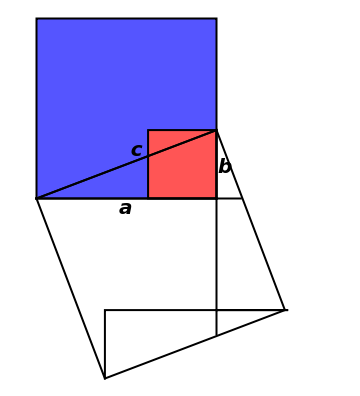
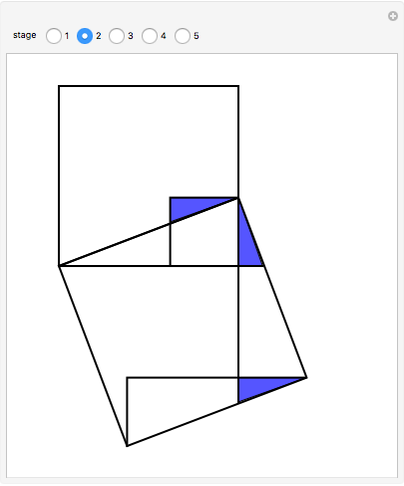
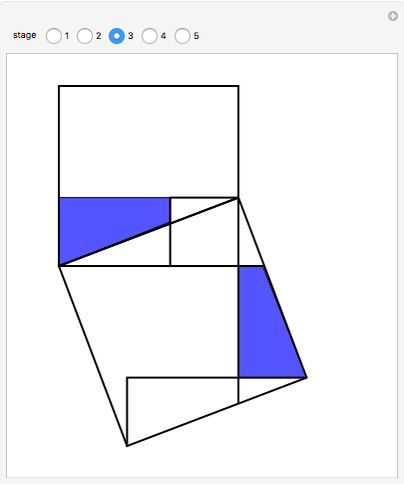
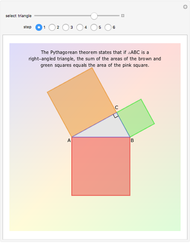
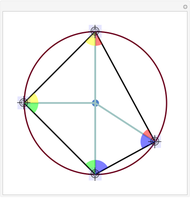
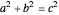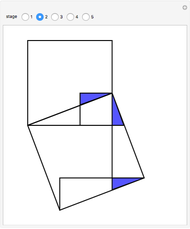
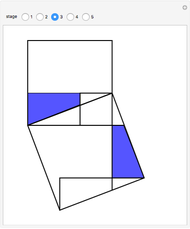
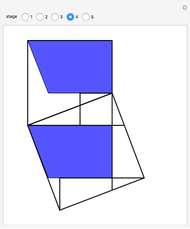
This Demonstration constructs a proof of Pythagoras's theorem, which states that in a right-angled triangle with adjacent sides of length and and hypotenuese of length , . Geometrically this says that the sum of the areas of the two squares of side and equals the area of the square of side . The proof works by splitting up the squares into pieces and matching pairs of equal area.

[more]

1. Part of the square covers the square, so its two pieces must be matched to pieces of equal area twice. The original triangle is part of both the square and the square, so it matches itself, but the trapezoidal piece inside the square must still be matched once (as part of the last step).

2. These three triangles are identical.

3. These two trapezoids have the same area.

4. These two trapezoids also have the same area.

5. There are two pieces left in the square (blue). They match the two pieces of the original triangle, which has the same area as the other half of the rectangle formed from the original triangle (green). The two pieces there match the remaining two pieces in the square (blue).

[less]

Contributed by: Jon Perry (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send