Mathematica MathWorld Wolfram Science More »

The Eutrigon Theorem


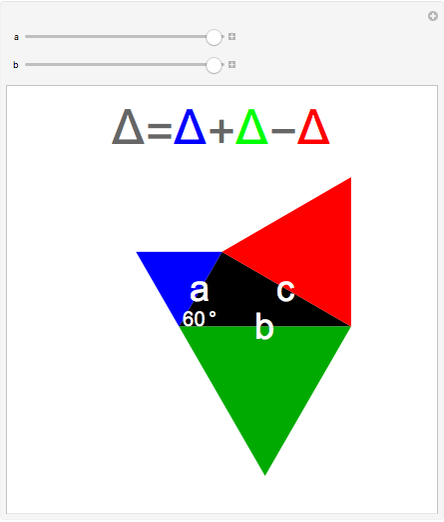
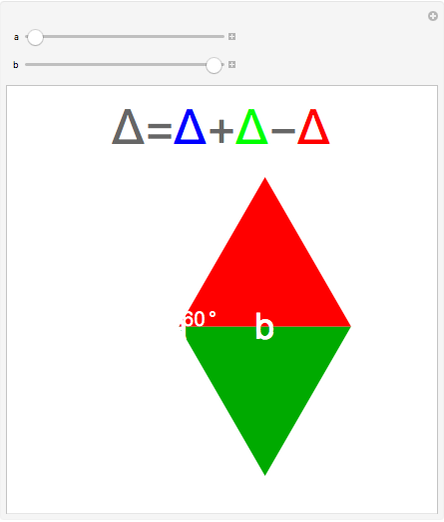
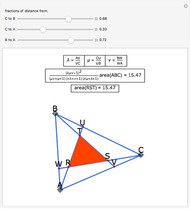
	The black central triangle with one angle equal to 60° is called a eutrigon. The areas of equilateral triangles constructed on the three faces , , and obey the eutrigon theorem, which gives the area of the black triangle in terms of the areas of the other three triangles.


	Contributed by: S. M. Blinder With corrections contributed by Liam Bauress and Oscar Chavez

Here is a quick proof: The area of an equilateral triangle with side

. By the law of sines, the area of a eutrigon is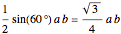

. The law of cosines gives

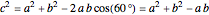, because

. Multiplying by

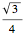gives the statement of the theorem.

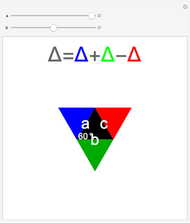
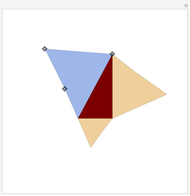
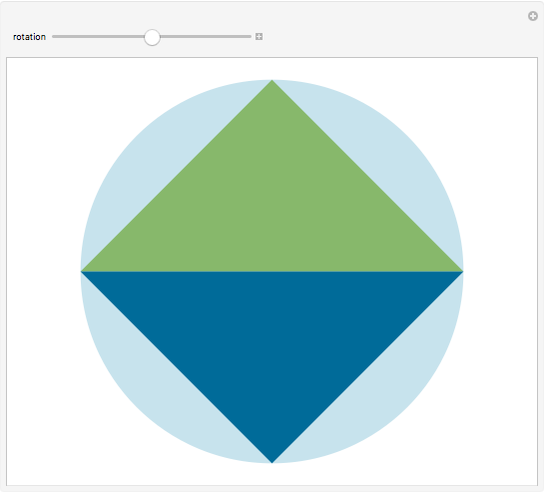
Snapshot 1: when

, the figure reduces to four equal equilateral triangles. The validity of the theorem then becomes trivial

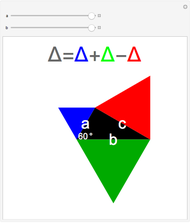
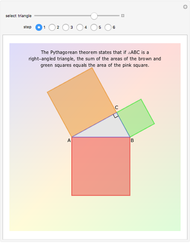
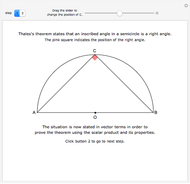
Snapshot 2: when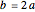

, the eutrigon becomes a 30-60-90 right triangle. By Pythagoras' theorem,

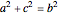, implying that the black triangle is twice the area of the blue triangle

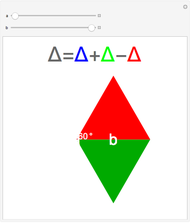
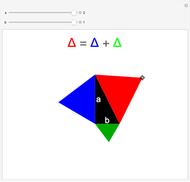
Snapshot 3: a degenerate case, with

, which collapses the eutrigon

Reference: "The Eutrigon Theorem - a new* twin to the theorem of Pythagoras" on this website.

Contributed by: S. M. Blinder

With corrections contributed by Liam Bauress and Oscar Chavez

Report an issue »

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

RSS

Atom