Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Parallelogram with Vertices on Two Circles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

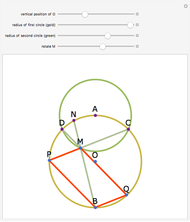
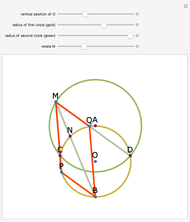
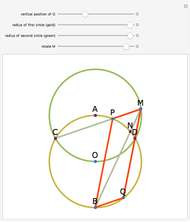
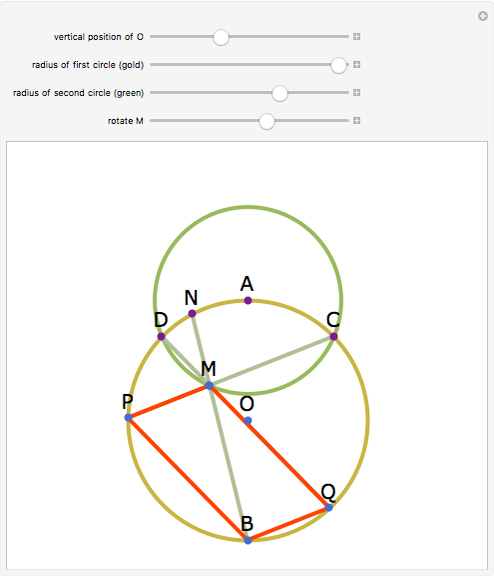
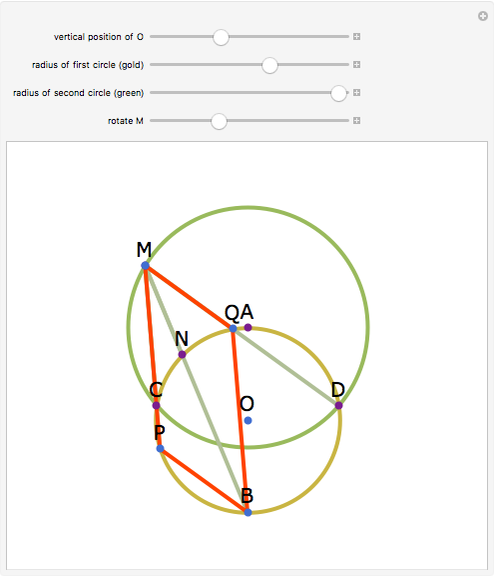
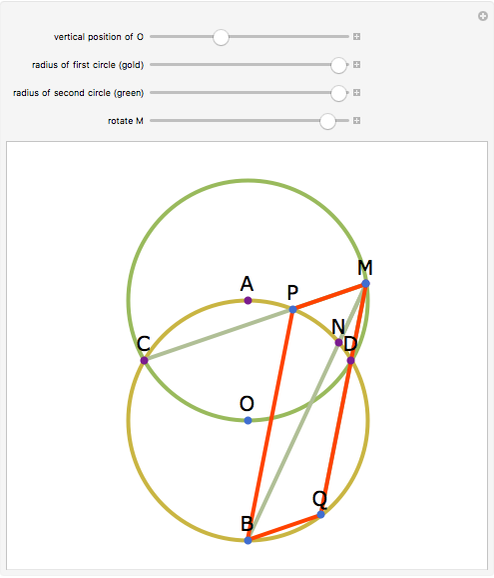
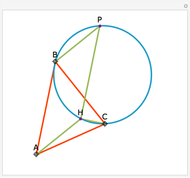
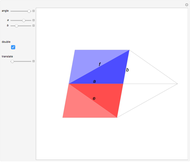
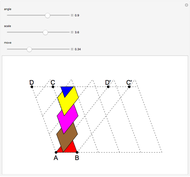
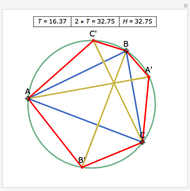
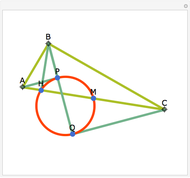
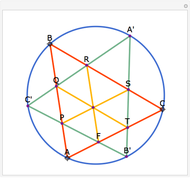
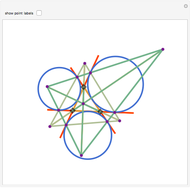
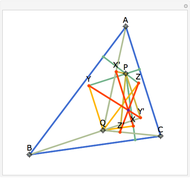
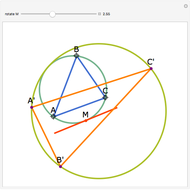
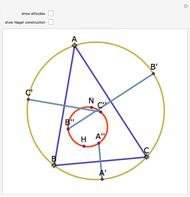
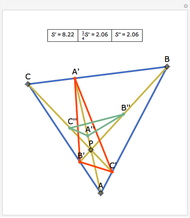
Let a circle have diameter AB and let M be a point on another circle with center at A. Let the circles intersect at C and D. Let BM, CM, and DM intersect the first circle at N, P, and Q, respectively. Then MPBQ is a parallelogram.

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

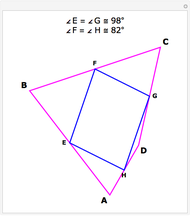
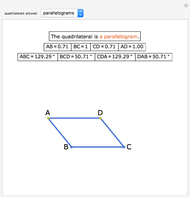
Snapshots

Details

See problem 2666 inCrux Mathematicorum 28(7), 2002 pp. 462-3.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send