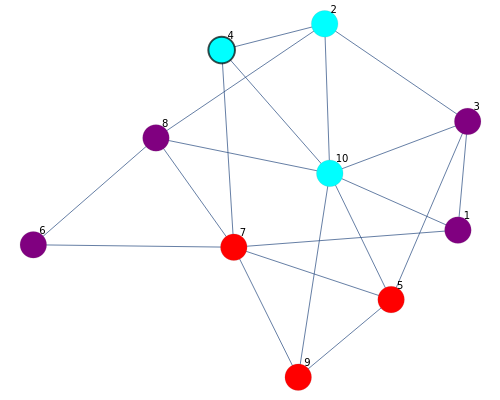
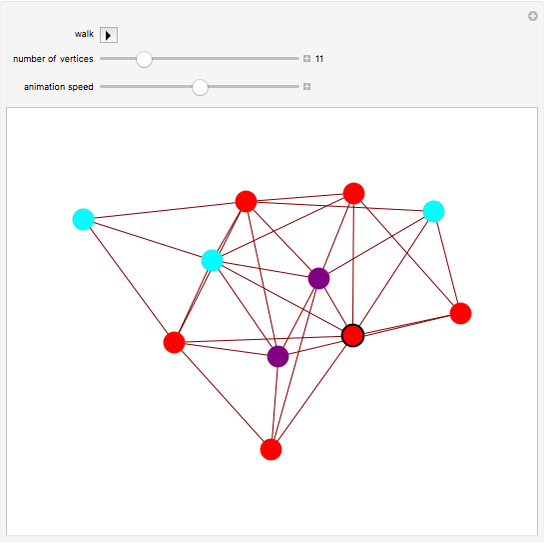
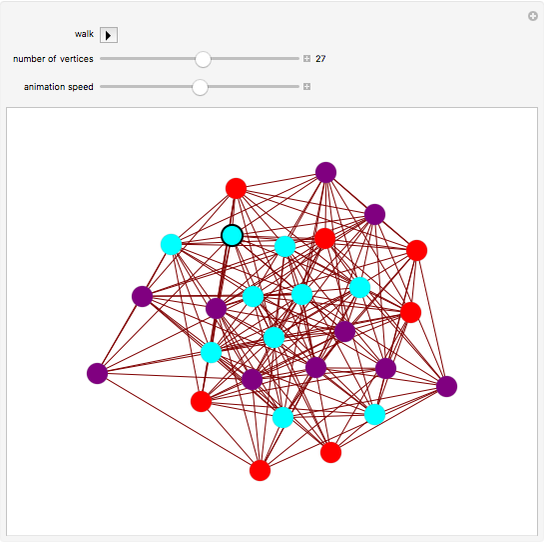
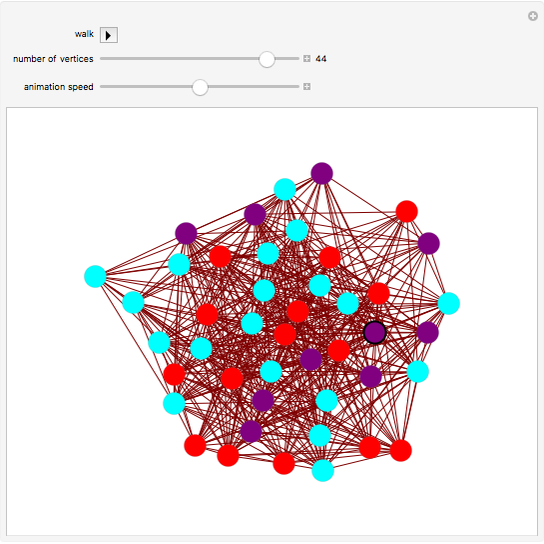
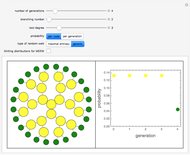
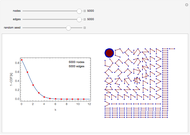
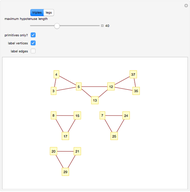
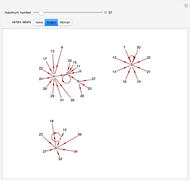
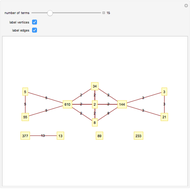
Vertices of a random graph are assigned colors to represent Rock (Red), Paper (Purple), and sCissors (Cyan). A "walker" (black circular outline) takes a random walk along the edges of the graph. As it moves from vertex to vertex , if beats (in the sense of the game Rock-Paper-Scissors: rock beats scissors, scissors beats paper, paper beats rock), then vertex is changed to the color of . (If beats , no change is made.)