An American High School Mathematics Examination Question

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
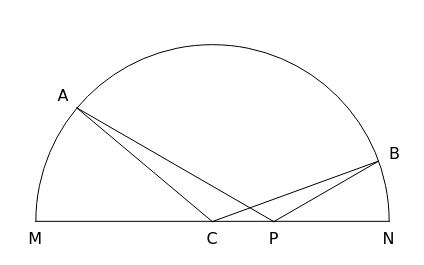
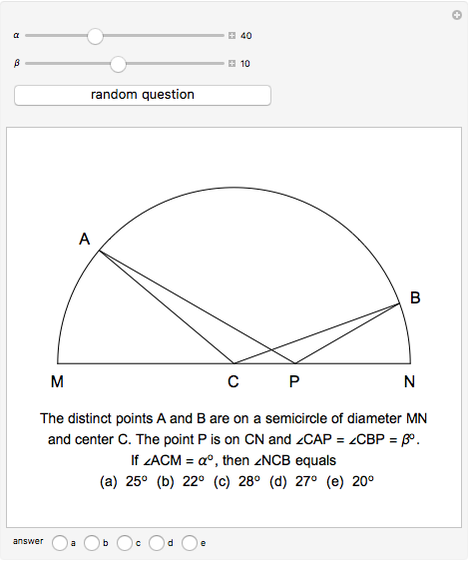
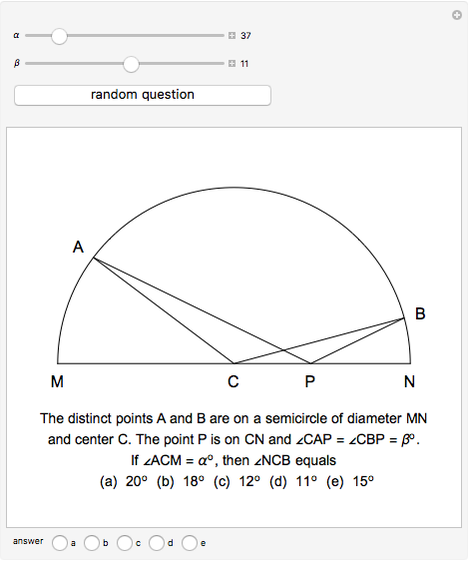
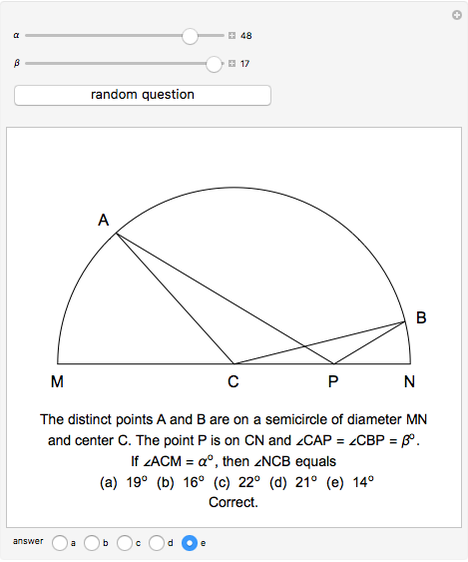
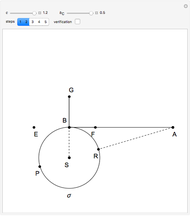
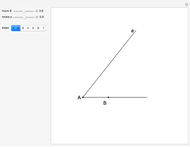
This Demonstration is an attempt to produce multiple-choice questions such as those posed on various examinations like the AHSME (American High School Mathematics Examination) and the AIME (American Invitational Mathematics Examination), or at the Australian mathematics competition and the European Mathematical Kangaroo. Here is a generalization of question 30 on the 1983 AHSME.
Contributed by: Izidor Hafner (April 2016)
Open content licensed under CC BY-NC-SA
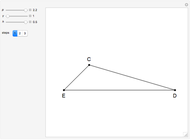
Snapshots
Details
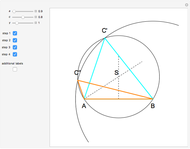
Solution of problem 30:  ,
,  [1, pp. 72].
[1, pp. 72].
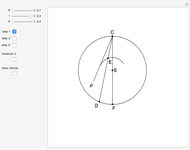
In  and
and  , we have (in the order given) the condition angle-side-side. By the "ASS theorem", the angles
, we have (in the order given) the condition angle-side-side. By the "ASS theorem", the angles  and
and 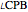 are either equal or supplementary. Since these triangles are not congruent (
are either equal or supplementary. Since these triangles are not congruent ( ), we must have that
), we must have that  and
and 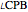 are supplementary. From
are supplementary. From  we compute
we compute
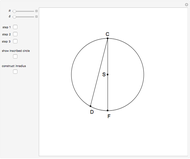
 .
.
Thus,  and
and
 .
.
Reference
[1] G. Berzsenyi and S. B. Maurer, eds., The Contest Problem Book V, Washington, DC: Mathematical Association of America, 1998.
Permanent Citation