An Enneper-Weierstrass Minimal Surface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
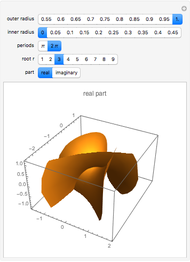
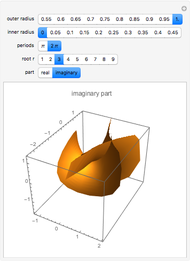
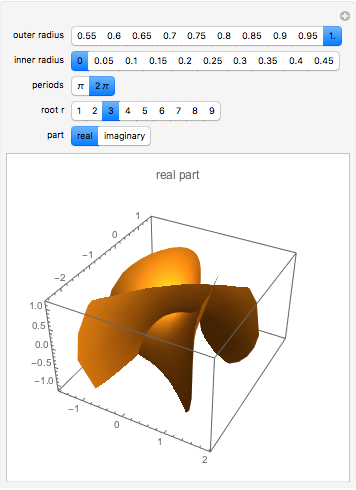
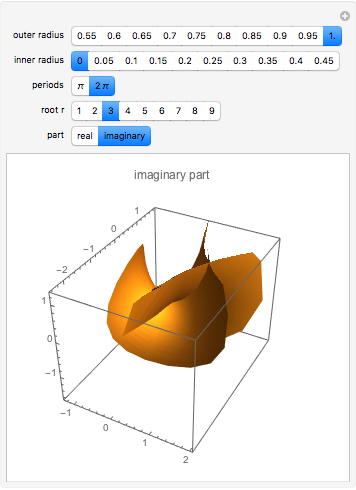
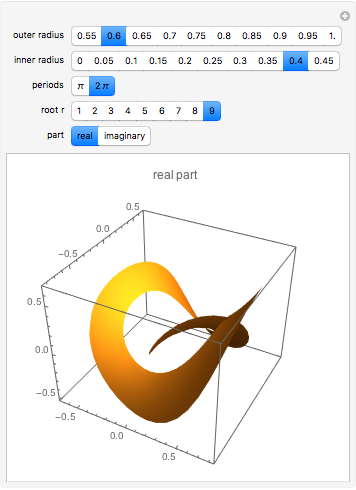
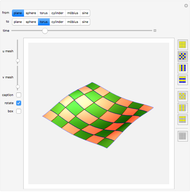
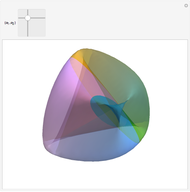
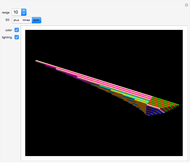
A minimal surface has zero mean curvature. An Enneper-Weierstrass parametrization for such a surface is based on two suitably defined holomorphic functions  and
and  . The functions chosen here are
. The functions chosen here are  and
and  . Embedding in
. Embedding in  is given by the indefinite integrals
is given by the indefinite integrals  , where
, where  ,
,  and
and  . The surface shown is the parametric plot of the real and imaginary parts of the
. The surface shown is the parametric plot of the real and imaginary parts of the  as
as  ranges over an annulus.
ranges over an annulus.
Contributed by: Michael Schreiber (March 2011)
Open content licensed under CC BY-NC-SA
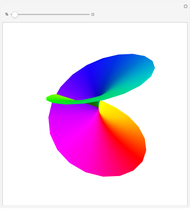
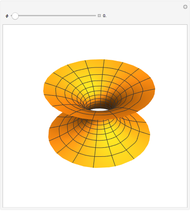
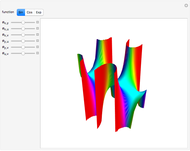
Snapshots
Details
detailSectionParagraphPermanent Citation
"An Enneper-Weierstrass Minimal Surface"
http://demonstrations.wolfram.com/AnEnneperWeierstrassMinimalSurface/
Wolfram Demonstrations Project
Published: March 7 2011