Minimal and Maximal Surfaces Generated by the Holomorphic Function log(z)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
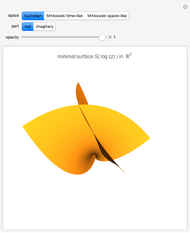
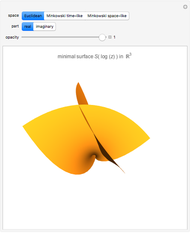
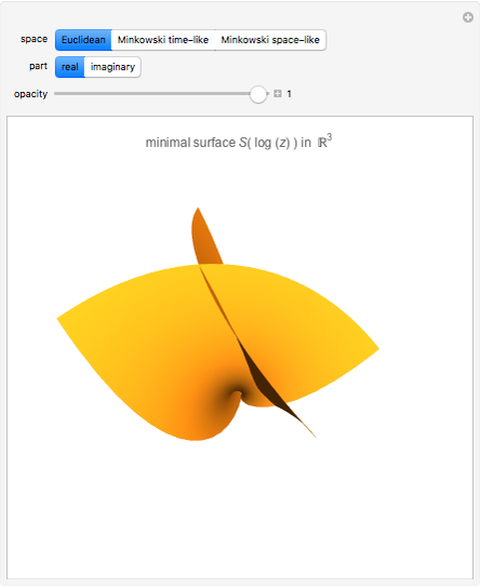
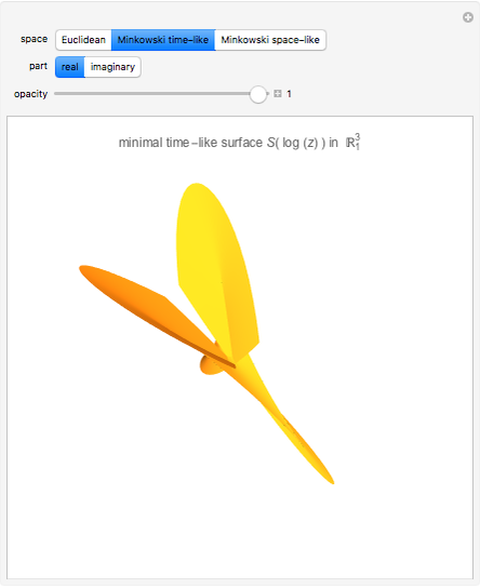
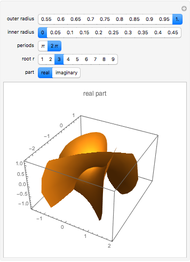
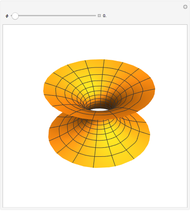
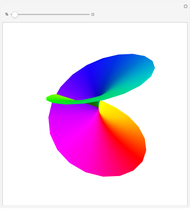
The holomorphic function 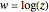 in the Gauss plane generates a minimal surface in Euclidean space
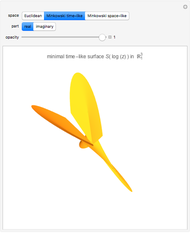
in the Gauss plane generates a minimal surface in Euclidean space 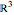 and a minimal time-like surface in Minkowski space
and a minimal time-like surface in Minkowski space 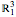 ; the same holomorphic function in the Lorentz plane generates a maximal space-like surface in
; the same holomorphic function in the Lorentz plane generates a maximal space-like surface in 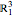 .
.
Contributed by: Georgi Ganchev and Radostina Encheva (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Any minimal surface in Euclidean space 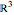 or any minimal time-like surface in Minkowski space
or any minimal time-like surface in Minkowski space 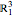 is generated by a holomorphic function
is generated by a holomorphic function 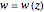 in the Gauss plane
in the Gauss plane  ; any maximal space-like surface in
; any maximal space-like surface in 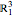 is generated by a holomorphic function in the Lorentz plane
is generated by a holomorphic function in the Lorentz plane  .
.
G. Ganchev, "Canonical Weierstrass Representation of Minimal Surfaces in Euclidean Space," arxiv.org/abs/0802.2374.
G. Ganchev, "Canonical Weierstrass Representation of Minimal and Maximal Surfaces in the Three-Dimensional Minkowski Space," arxiv.org/abs/0802.2632.
Permanent Citation