Exploring Surface Curvature and Differentials

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
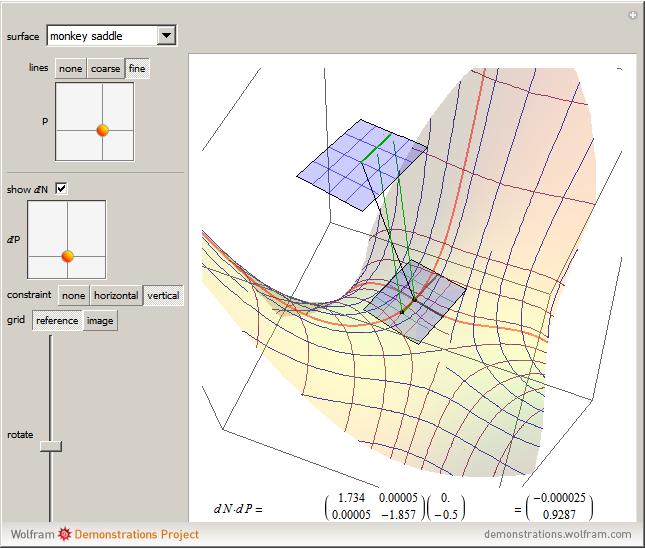
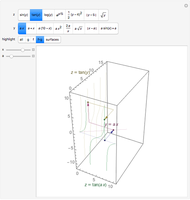
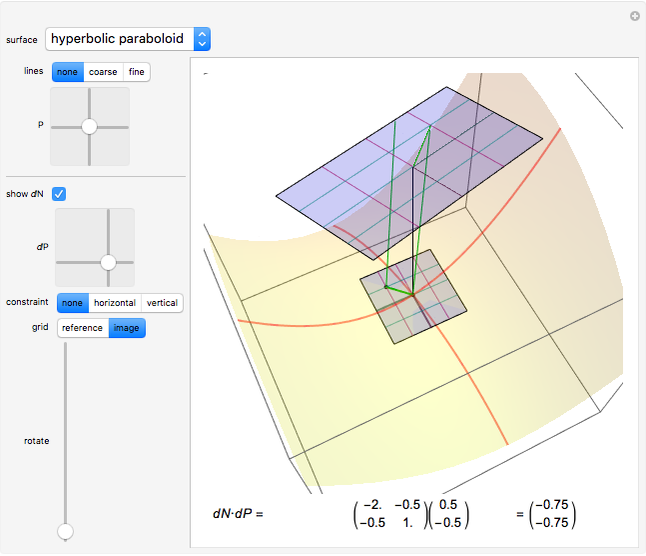
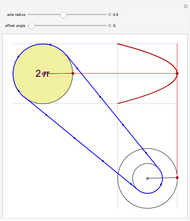
This Demonstration shows the relationship between the principal curvatures of a surface and the differential 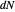 of the unit normal of the surface. The differential
of the unit normal of the surface. The differential 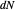 at a point may be viewed as a linear transformation of the tangent plane at the point, since the derivative of the unit normal is orthogonal to the normal. The eigenvalues of
at a point may be viewed as a linear transformation of the tangent plane at the point, since the derivative of the unit normal is orthogonal to the normal. The eigenvalues of 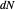 are the negatives of the principal curvatures of the surface at the point, and correspondingly the eigenvectors are the principal directions. At a point
are the negatives of the principal curvatures of the surface at the point, and correspondingly the eigenvectors are the principal directions. At a point 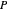 one may rotate an orthogonal basis for the tangent plane to diagonalize the matrix for
one may rotate an orthogonal basis for the tangent plane to diagonalize the matrix for 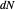 by aligning the basis with the principal directions. One may see how a small tangent vector
by aligning the basis with the principal directions. One may see how a small tangent vector 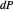 is mapped by
is mapped by 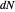 and compare it to the actual difference in the normals at the points
and compare it to the actual difference in the normals at the points  and
and 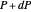 .
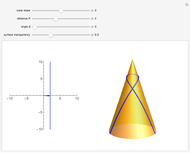
. The lines that are drawn on the surface are lines of curvature, which are curves whose tangents at every point match one of the principal directions.
The lines that are drawn on the surface are lines of curvature, which are curves whose tangents at every point match one of the principal directions.
Contributed by: Michael Rogers (Oxford College of Emory University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In addition to the principal curvatures of a surface, this Demonstration illustrates geometrically several interesting concepts: differentials and local linear approximation, linear transformations, eigenvectors and eigenvalues, the orthogonal diagonalization of symmetric matrices, and the relation of the rotation of the normal vector of a surface to the curvature. Note the negative of 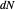 is called the shape operator.
is called the shape operator.
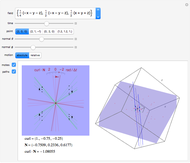
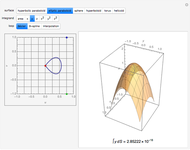
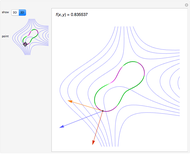
To explore 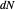 as a linear transformation: move
as a linear transformation: move 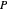 to a desired location. Move
to a desired location. Move 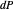 to change the tangent vector at
to change the tangent vector at 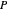 ; the motion of
; the motion of  may be constrained to move horizontally or vertically. The image vector
may be constrained to move horizontally or vertically. The image vector 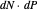 is drawn in the plane at the end of the normal at
is drawn in the plane at the end of the normal at  . The image plane may be drawn with the same basis as the tangent plane (the "reference" grid) or with the image of the basis under
. The image plane may be drawn with the same basis as the tangent plane (the "reference" grid) or with the image of the basis under  (the "image" grid). The basis of the tangent plane may be rotated with the slider. By rotating the basis to align with the principal directions, the matrix of
(the "image" grid). The basis of the tangent plane may be rotated with the slider. By rotating the basis to align with the principal directions, the matrix of 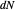 may be diagonalized. In the display, numerical values of
may be diagonalized. In the display, numerical values of 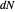 ,
,  , and
, and 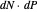 are given with respect to the basis of the tangent plane.
are given with respect to the basis of the tangent plane.
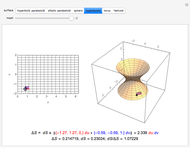
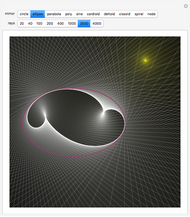
The display: the lines on the surface show the principal configuration (lines of curvature). At the point 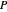 , the unit normal vector is drawn in black, and the lines of curvature through
, the unit normal vector is drawn in black, and the lines of curvature through 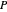 are drawn on the surface. For the point
are drawn on the surface. For the point  , the normal is drawn twice in green, both at
, the normal is drawn twice in green, both at 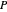 and at
and at 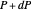 . There are two things to observe: the angle between the normals and the displacement between the tips of the normals. On the one hand, if the change
. There are two things to observe: the angle between the normals and the displacement between the tips of the normals. On the one hand, if the change 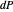 is parallel to a principal direction, then the angle rotated will be approximately the negative of the curvature times the distance moved; on the other hand, the displacement will be approximately equal to
is parallel to a principal direction, then the angle rotated will be approximately the negative of the curvature times the distance moved; on the other hand, the displacement will be approximately equal to 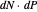 . Basis vectors are highlighted in the tangent plane and the image grid.
. Basis vectors are highlighted in the tangent plane and the image grid.
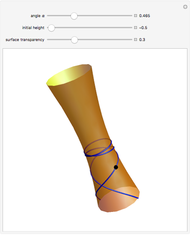
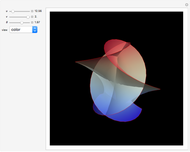
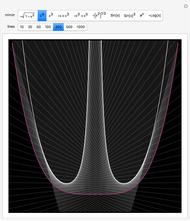
Umbilic points are points where the normal curvature is the same in all directions and 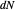 is scalar. Some of them are bookmarked in the + menu in the upper left. Darboux first classified curvature umbilics into three types, now sometimes called lemons, stars, and monstars (or lemonstars). For more information, see G. Darboux, "Note VII: Sur la forme des lignes de courbure dans la voisinage d'un ombilic," Leçons sur la Théorie Générale des Surfaces, Vol. 4, Paris: Gauthier–Villars, 1896 pp. 448–465.
is scalar. Some of them are bookmarked in the + menu in the upper left. Darboux first classified curvature umbilics into three types, now sometimes called lemons, stars, and monstars (or lemonstars). For more information, see G. Darboux, "Note VII: Sur la forme des lignes de courbure dans la voisinage d'un ombilic," Leçons sur la Théorie Générale des Surfaces, Vol. 4, Paris: Gauthier–Villars, 1896 pp. 448–465.
Questions for exploration:
When the matrix of  is diagonalized, the image grid is a rectangle. Why?
is diagonalized, the image grid is a rectangle. Why?
When the vector 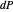 is rotated, which way does its image rotate? When is it in the same direction and when is it different? Is it ever the case that the image of
is rotated, which way does its image rotate? When is it in the same direction and when is it different? Is it ever the case that the image of  does not rotate but changes length?
does not rotate but changes length?
Sometimes the tip of the image vector 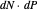 stays close to the tip of the green normal based at
stays close to the tip of the green normal based at 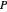 , and sometimes it does not. Why? To clarify: since the normal vectors are unit length, the green vector rotates away from the plane. One expects the tips to lie on a line approximately parallel to the normal. In other words, if the viewpoint is adjusted so the reference grids align, one tip should be on top of the other. Sometimes they are closer, and sometimes not.
, and sometimes it does not. Why? To clarify: since the normal vectors are unit length, the green vector rotates away from the plane. One expects the tips to lie on a line approximately parallel to the normal. In other words, if the viewpoint is adjusted so the reference grids align, one tip should be on top of the other. Sometimes they are closer, and sometimes not.
Is it obvious—in the visual sense—that the principal curvatures and the eigenvalues of 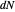 have opposite signs?
have opposite signs?
Show that if 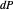 traces the unit circle
traces the unit circle  in the tangent plane, the coordinates being with respect to the orthonormal basis of principal directions, then its image
in the tangent plane, the coordinates being with respect to the orthonormal basis of principal directions, then its image  traces the ellipse
traces the ellipse  , where
, where 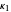 and
and 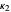 are the principal curvatures. Deduce Euler's formula for the normal curvature
are the principal curvatures. Deduce Euler's formula for the normal curvature  in the direction
in the direction 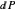 , namely,
, namely, 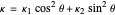 .
.
Permanent Citation