Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

An Infinitely Colorable Set of 3D Regions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

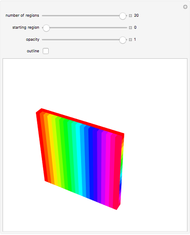
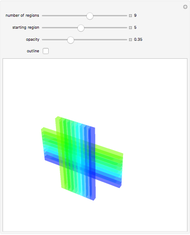
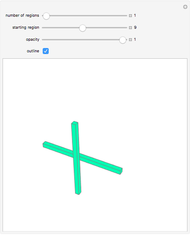
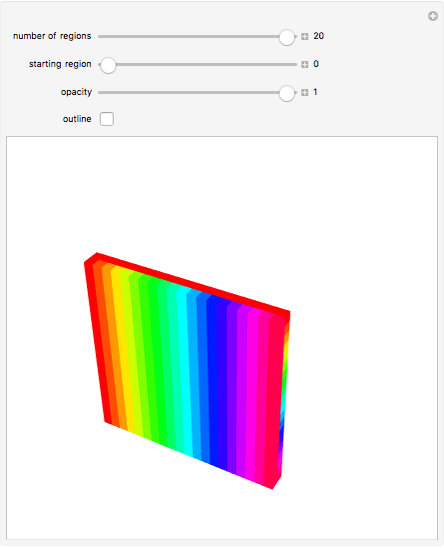
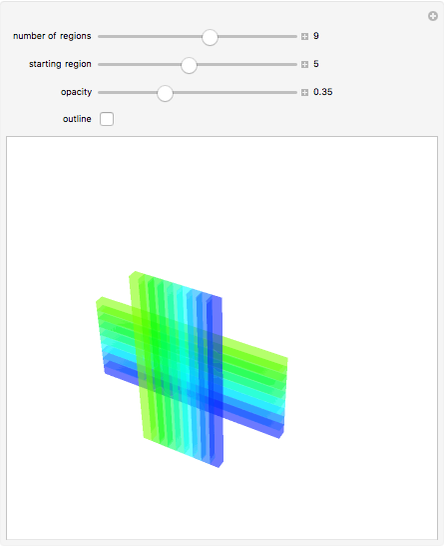
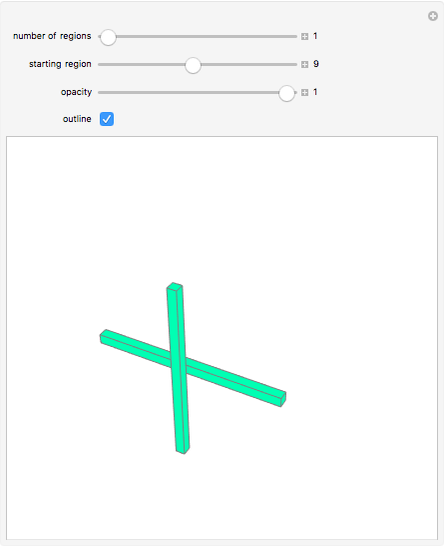
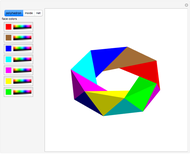
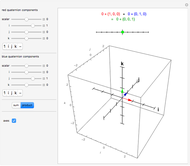
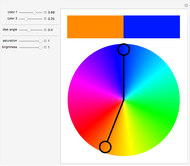
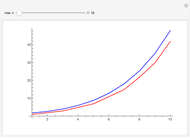
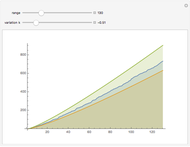
Suppose that if two regions touch, then they should have different colors. How many colors suffice? In the plane, four colors are sufficient. In 3D, the set of regions shown requires an infinite number of colors.

Contributed by: Jon Perry (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send