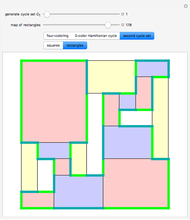
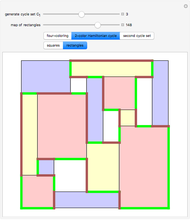
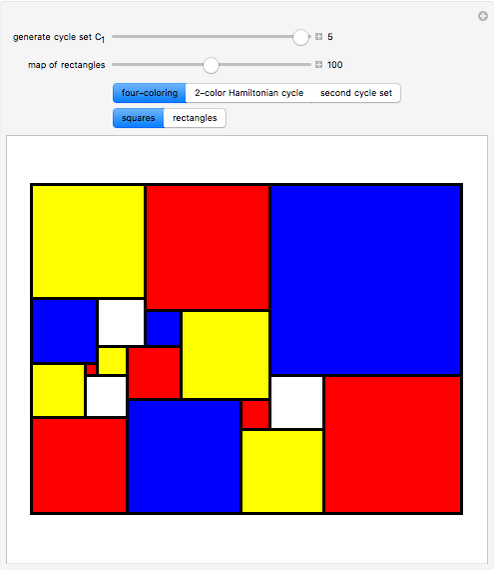
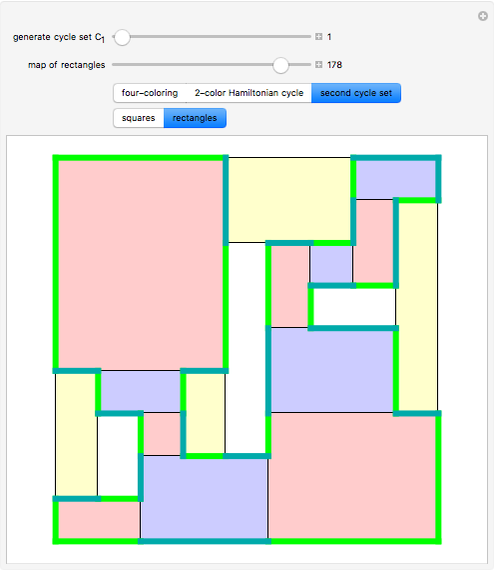
Mondrian Four-Coloring
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
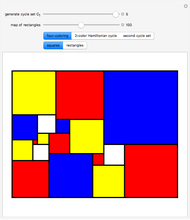
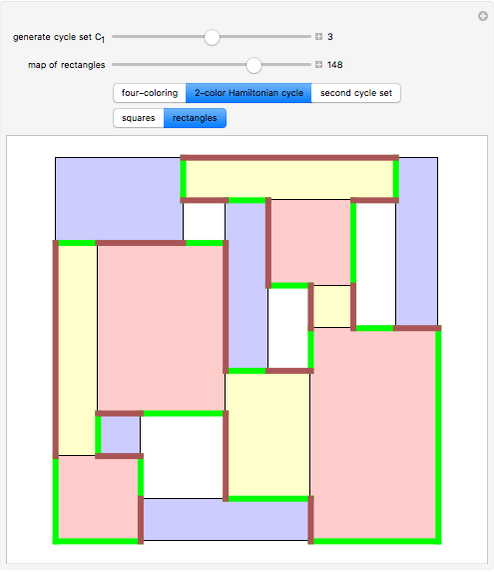
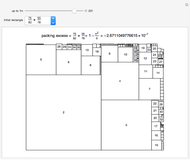
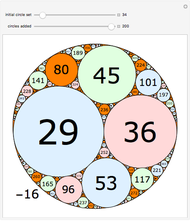
Any planar map can be colored with four colors so that no two regions of the same color touch each other.
[more]
Contributed by: Ed Pegg Jr (July 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Ed Pegg Jr, "Math Games: Square Packing," Dec. 1, 2003.
Permanent Citation