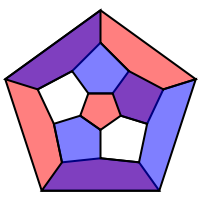
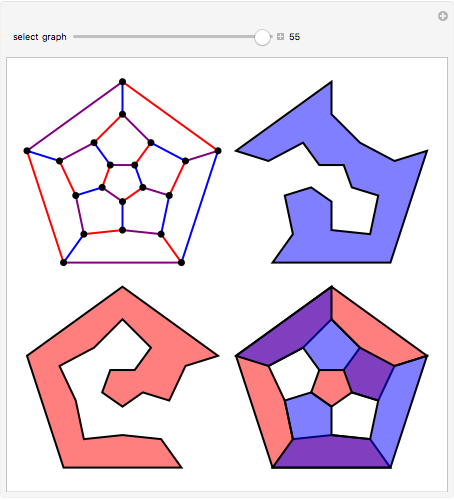
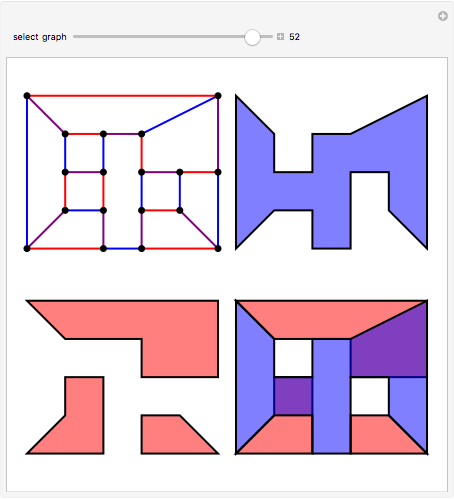
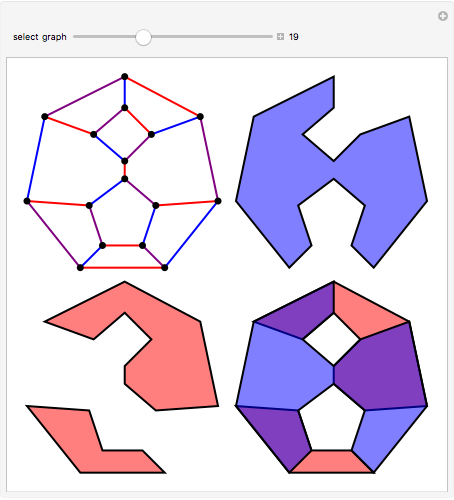
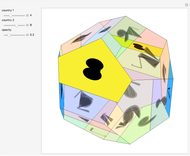
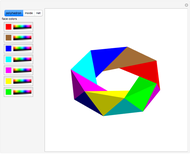
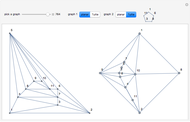
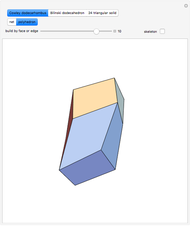
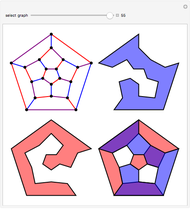
For 66 years, research on the four-color theorem was dominated by Tait's Hamiltonian graph conjecture: any cubic polyhedral graph has a Hamiltonian cycle. In a graph, cubic means that every vertex is incident with exactly three edges. Any planar graph can be made cubic by drawing a small circle around any vertex with valence greater than three and eliminating the original vertex. Tutte, in 1946, found the first counterexample to Tait's conjecture.