Arc Length of Cycloid
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
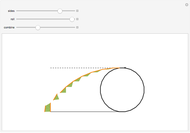
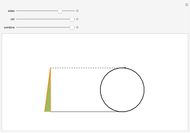
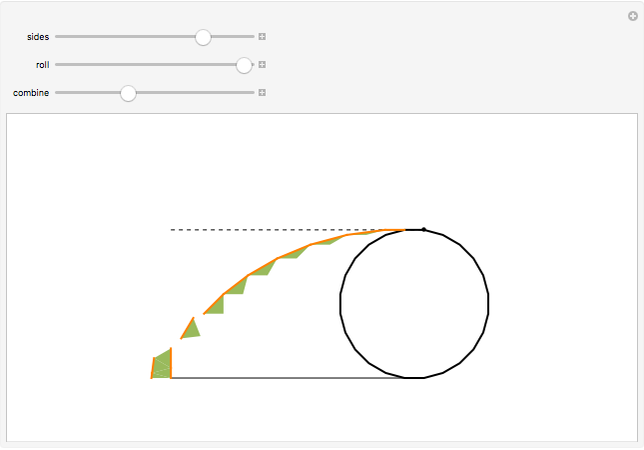
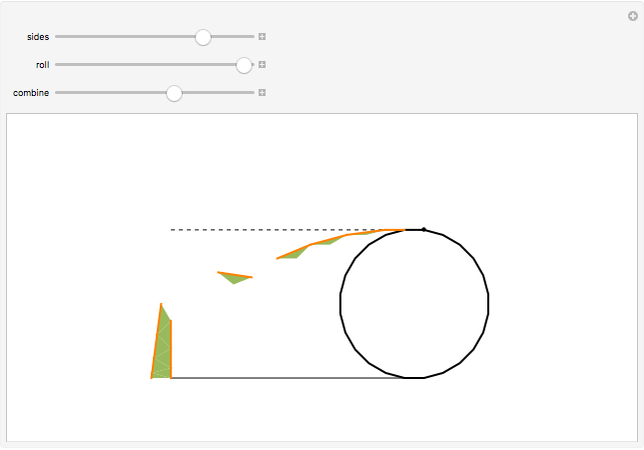
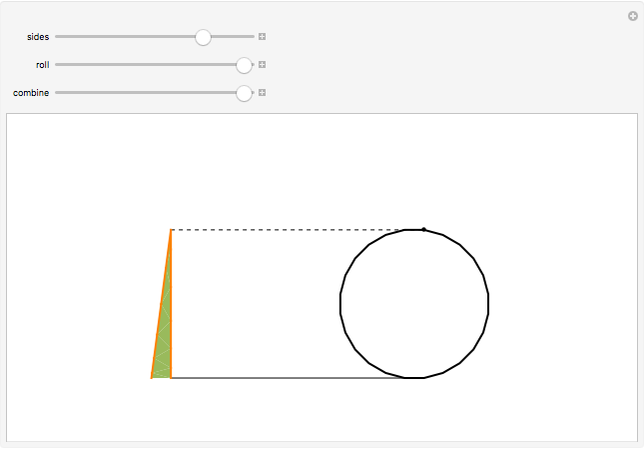
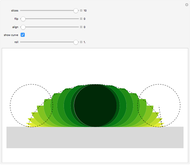
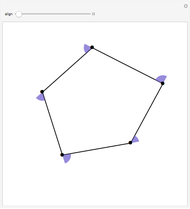
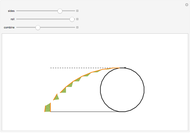
A polygon  rolls on a line
rolls on a line  . The positions of a vertex when
. The positions of a vertex when  has a side flush with
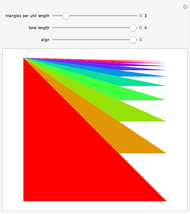
has a side flush with  form a polygonal path (orange). The orange segments are the base sides of green isosceles triangles. When you drag the "combine" slider, the green triangles combine to form a right triangle with height
form a polygonal path (orange). The orange segments are the base sides of green isosceles triangles. When you drag the "combine" slider, the green triangles combine to form a right triangle with height  , the diameter of incircle of the polygon. Hence, the length of the orange path is the sum of the height and the hypotenuse of this triangle.
, the diameter of incircle of the polygon. Hence, the length of the orange path is the sum of the height and the hypotenuse of this triangle.
Contributed by: Okay Arik (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation