Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Area under the Exponential Curve

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

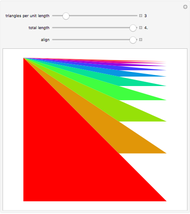
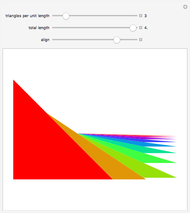
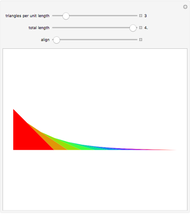
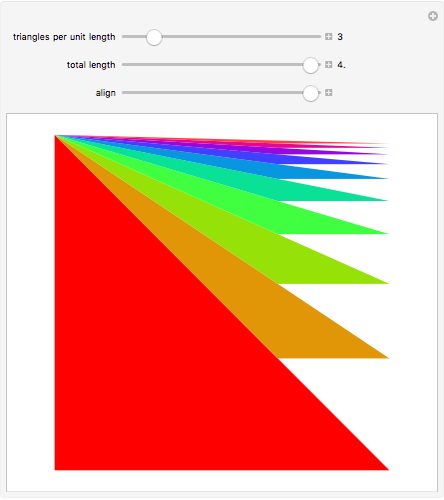
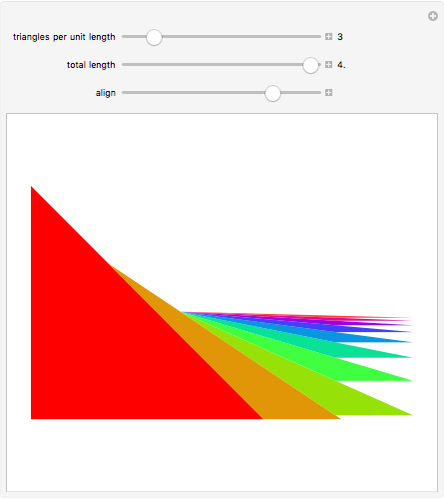
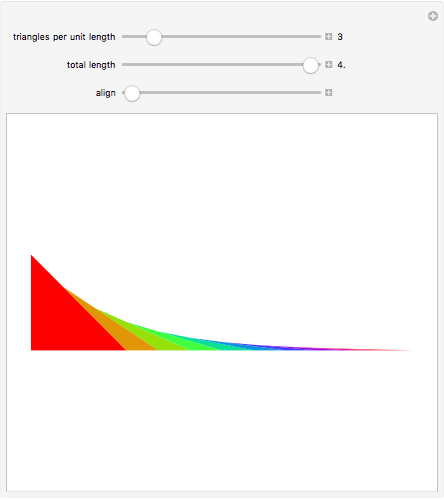
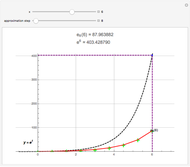
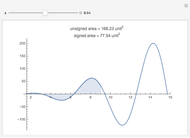
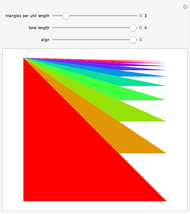
Consider a curve consisting of segments joining the points , where and . The region under this curve is broken into triangular pieces by extending the segments to the axis. Each extended segment projects onto a segment of length 1 on the axis because .

[more]

You can align these triangles one on top of the other above the interval [0,1] on the axis using the "align" slider. You can control the constant using the "triangles per unit length" slider.

Let . As and tend to infinity, the curve approaches the exponential curve . The "total length" slider controls the length of the interval. As the total length tends to infinity, the aligned triangles fill the unit square of area 1.

[less]

Contributed by: Okay Arik (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

For more information visit "Visual Calculus by Mamikon".

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send