Area under a Parabola by Symmetries

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
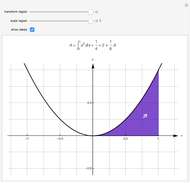
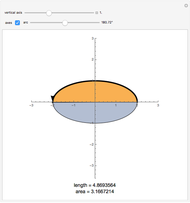
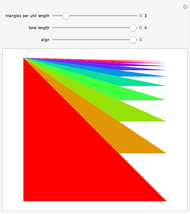
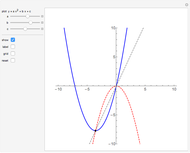
The area  of the region
of the region 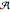 under the curve
under the curve 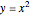 over the interval
over the interval  equals the area of the region
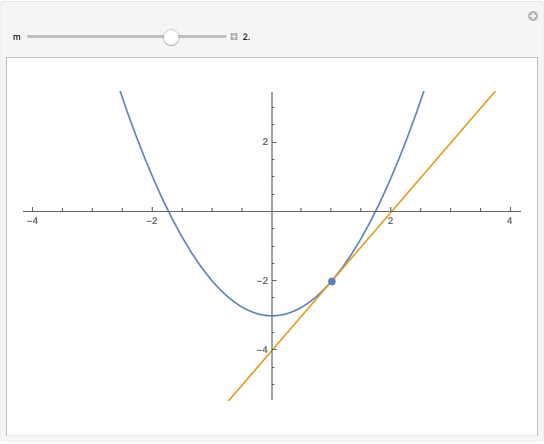
equals the area of the region  (in light blue) under the curve and above the line
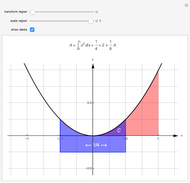
(in light blue) under the curve and above the line  . The area-preserving shear-translation symmetry
. The area-preserving shear-translation symmetry  of the curve moves the region
of the curve moves the region  to a region whose area is one-quarter plus twice the area of the region
to a region whose area is one-quarter plus twice the area of the region  under the curve over the interval
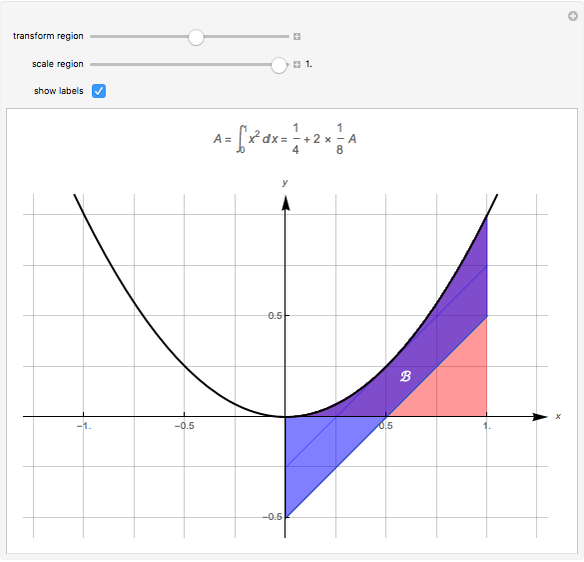
under the curve over the interval 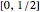 . The scaling symmetry
. The scaling symmetry 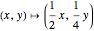 of the curve maps
of the curve maps 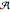 to
to  and reduces the area by the factor
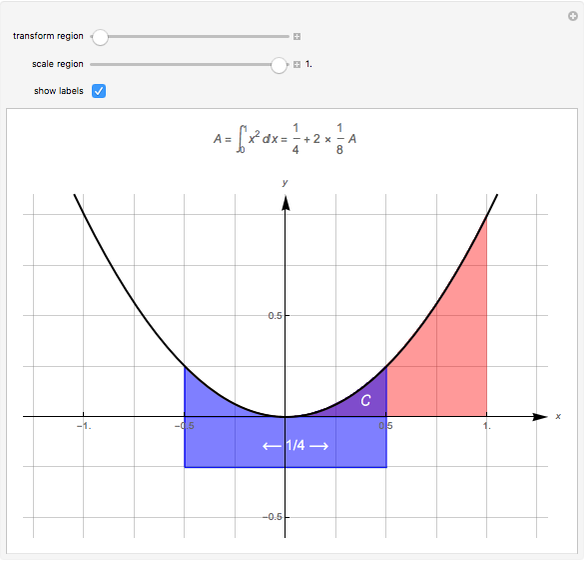
and reduces the area by the factor  . Thus
. Thus  so
so 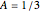 .
.
Contributed by: Gerry Harnett (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
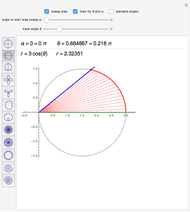
Like any parabola, the parabola 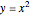 admits two one-parameter families of symmetries. One family consists of the scale-scale transformations
admits two one-parameter families of symmetries. One family consists of the scale-scale transformations  , where
, where 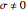 , which scales areas by the factor
, which scales areas by the factor  . The other family consists of the "shear-translation" symmetries given by
. The other family consists of the "shear-translation" symmetries given by  , where
, where  can be any real number; these transformations are area preserving. Applying certain subsets of these symmetries to the region
can be any real number; these transformations are area preserving. Applying certain subsets of these symmetries to the region 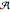 , we can see that the integral in question is exactly
, we can see that the integral in question is exactly 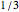 . This approach is easily extended to determine the area of a segment of any parabola. It thus provides a calculus-free proof of the quadrature of the parabola.
. This approach is easily extended to determine the area of a segment of any parabola. It thus provides a calculus-free proof of the quadrature of the parabola.
Permanent Citation