Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Bertrand's Box Paradox

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

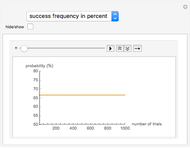
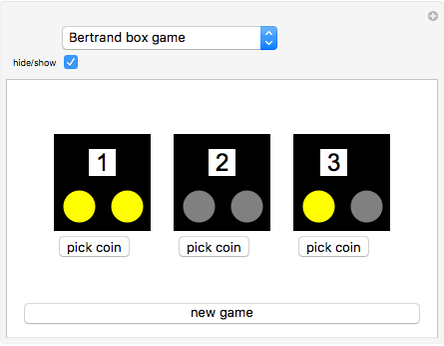
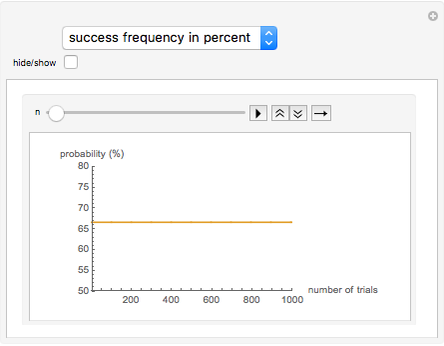
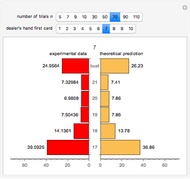
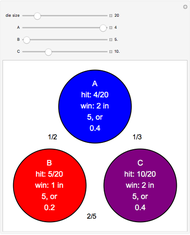
Consider three boxes. Box 1 contains two gold coins, box 2 contains two silver coins, and box 3 contains one gold and one silver coin. A box is chosen at random and then the coins in that box are chosen one at a time. Suppose that the first coin is gold. What is the probability that the second coin is also gold?

[more]

On the one hand, since the box chosen must be 1 or 3, it would seem that the next coin is either gold or silver with probability 1/2 for each.

On the other hand, it is more likely that the first gold coin comes from box 1 than box 3, leading to the probability 2/3 [1].

Which is it?

[less]

Contributed by: D. Meliga and S. Z. Lavagnino (January 2017)
Additional contribution by: G. Follo
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] Wikipedia. "Bertrand's Box Paradox." (Jan 20, 2017) en.wikipedia.org/wiki/Bertrand's_box _paradox.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send