Umbrella Quandary

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
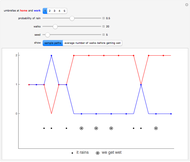
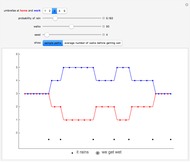
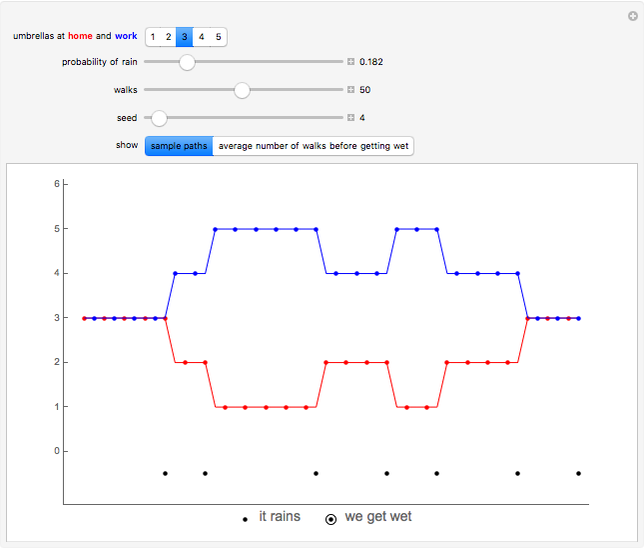
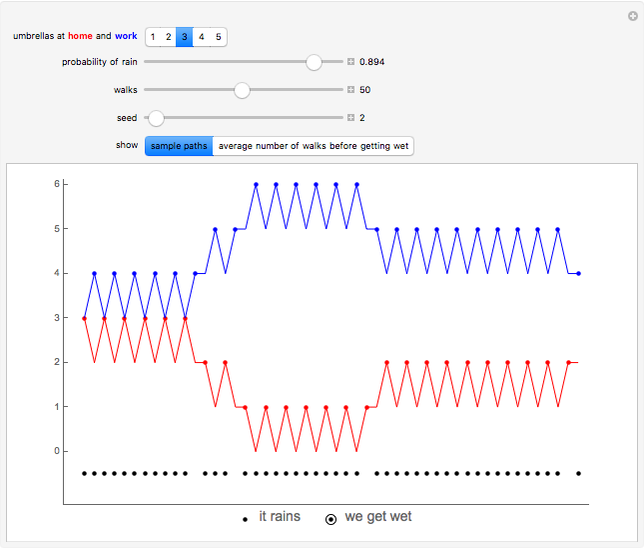
A man walks between home and work. Initially, he has some umbrellas at home and at work. If he is about to walk from home to work or from work to home and it is raining, he picks up an umbrella if such is available; if an umbrella is not available, he gets wet. To his disadvantage, the man does not take an umbrella if it is not raining; thus, it is likely that, sooner or later, all umbrellas will be at one of the locations, and so the man has a risk of getting wet. It is assumed that every time the man is about to walk, it is raining with a given probability, independently of history.
[more]
Contributed by: Heikki Ruskeepää (May 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
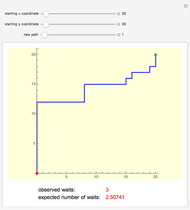
Snapshot 1: Let us briefly explain the first few steps in this small sample path. Initially, the man has one umbrella at home and one umbrella at work. The process starts at home (the first red point at level 1). When the man is about to walk from home to work, it is not raining and so he does not take an umbrella with him. When he is about to go back to home, it also does not rain. The next day, when he is leaving home it is raining, and so he takes an umbrella with him; the number of umbrellas at home thus decreases to zero and the number of umbrellas at work increases to two. When he is about to go home, it rains again. The third day, when he is about to go home, it rains. The fourth day, when he is about to go home, it is raining but he does not have any umbrellas at work; thus he gets wet.
Snapshot 2: If the probability of rain is small, the numbers of umbrellas at home and work remain constant for relatively long time intervals, because the man most of the time does not need to take an umbrella with him.
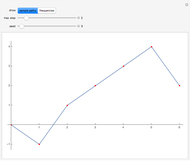
Snapshot 3: If the probability of rain is large, the numbers of umbrellas at home and work change very often, because the man, in most cases, takes an umbrella with him.
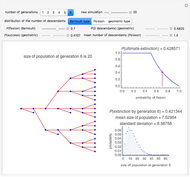
Snapshot 4: The average number of walks before getting wet is plotted when the probability of rain varies from 0.01 to 0.99 (in steps of 0.01; 20000 simulations were done for each value of the probability). The average is, of course, infinite when the probability of rain is zero, and it is also infinite when the probability of rain is 1 (because the man always carries an umbrella with him). The average number of walks before getting wet is smallest when the probability of rain is not small or large. For example, when the man initially has one umbrella at home and at work and the probability of rain is somewhere between 0.5 to 0.7, he gets wet, on the average, in about 12 walks.
The Demonstration is based on problem 10 in [1].
Reference
[1] P. J. Nahin, Digital Dice: Computational Solutions to Practical Probability Problems, Princeton: Princeton University Press, 2008.
Permanent Citation
"Umbrella Quandary"
http://demonstrations.wolfram.com/UmbrellaQuandary/
Wolfram Demonstrations Project
Published: May 21 2012