Bose-Einstein Condensation (Free Boson Gas)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
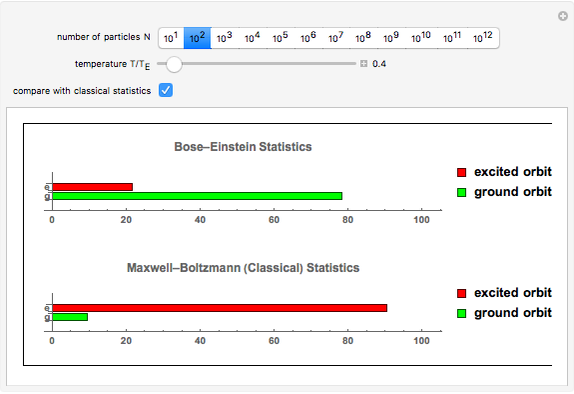
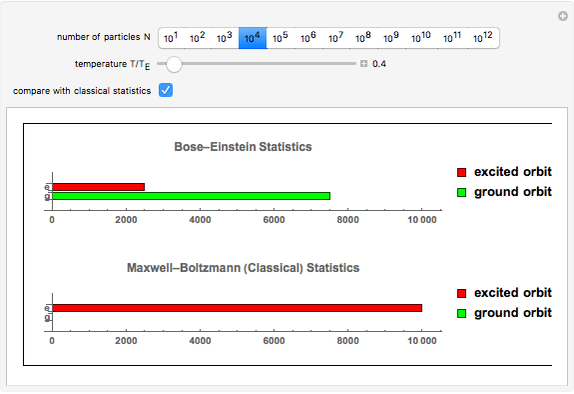
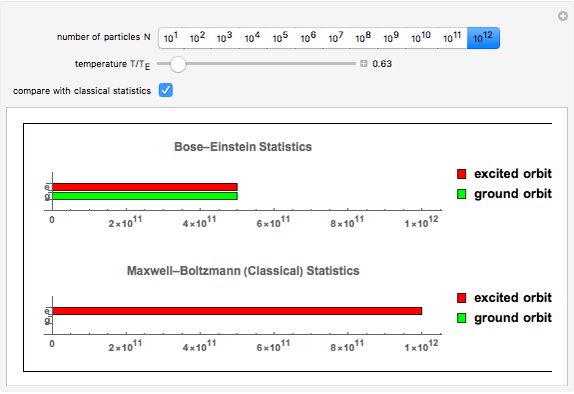
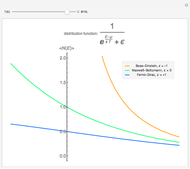
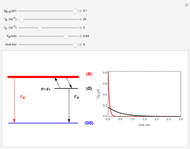
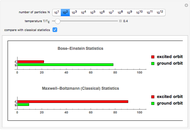
This Demonstration shows the thermal population of the ground orbital and all the excited orbitals for a gas of  free bosons as a function of temperature. The populations according to the classical Maxwell–Boltzmann statistics can also be shown. The temperature is measured in units of Einstein's condensation temperature.
free bosons as a function of temperature. The populations according to the classical Maxwell–Boltzmann statistics can also be shown. The temperature is measured in units of Einstein's condensation temperature.
Contributed by: Olivier Espinosa (Universidad Técnica Federico Santa María, Valparaíso, Chile) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
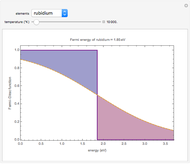
Einstein's condensation temperature is the temperature below which the ground orbital of a gas of free bosons is occupied by a macroscopic number of particles. This temperature is determined by the mass of the particles and their concentration. For atoms of Helium-4 in the liquid state this temperature is about 3.1 degrees Kelvin.
Note that in the case of Maxwell–Boltzmann statistics, the number of particles in the ground orbital is much smaller than the number of particles in excited orbitals for all temperatures except those much smaller than Einstein's temperature. For the parameters of snapshots 2 and 3, for instance, the classical occupations of the ground orbital are 10.3 and 5.2, respectively. Both numbers are too small in comparison with the total number of particles to be represented by a small bar.
For details of the statistical-mechanics calculations relevant to this problem, see
C. Kittel and H. Kroemer, Thermal Physics, New York: W. H. Freeman and Company, 1980.
Permanent Citation
"Bose-Einstein Condensation (Free Boson Gas)"
http://demonstrations.wolfram.com/BoseEinsteinCondensationFreeBosonGas/
Wolfram Demonstrations Project
Published: March 7 2011