Rabinovich-Fabrikant Equations
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
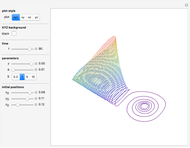
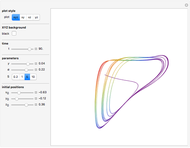
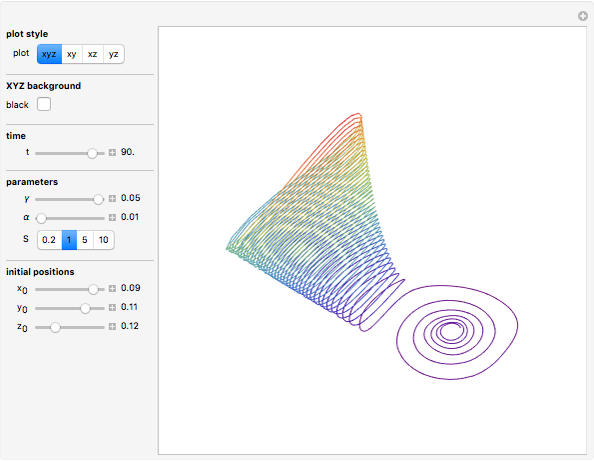
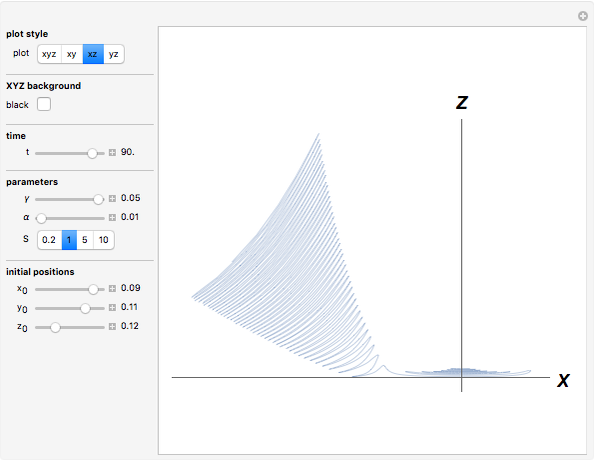
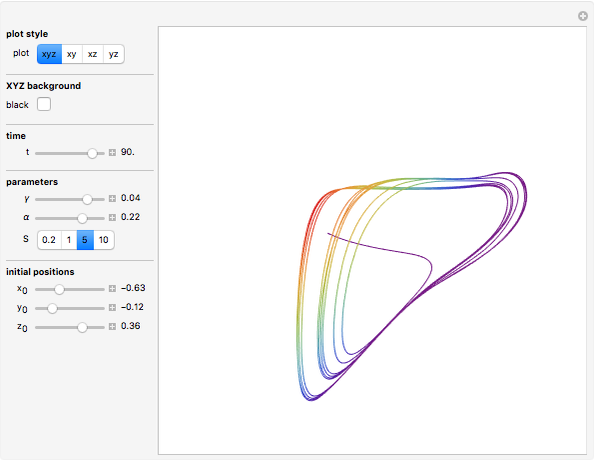
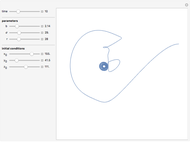
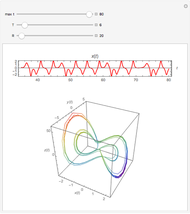
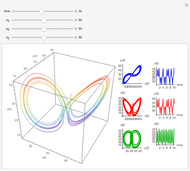
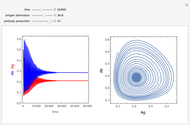
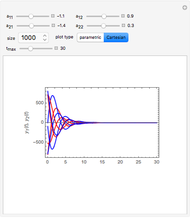
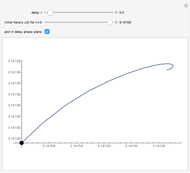
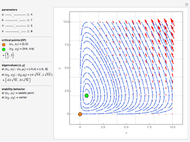
The Rabinovich–Fabrikant equations form a set of coupled, nonlinear, first-order differential equations given by:
[more]
Contributed by: Galen Craven (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Programming ideas on how to implement the plot style switching were taken from the Demonstration "A Study of the Dynamic Behavior of a Three-Variable Autocatalator" by Housam Binous and Zakia Nasri.
Permanent Citation