Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Closed-Form Approximations of Euler's Number e

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

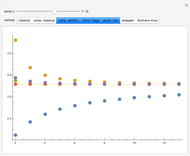
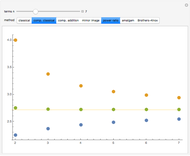
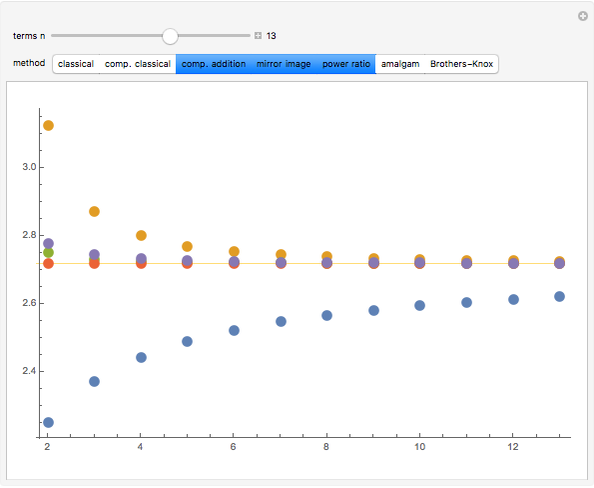
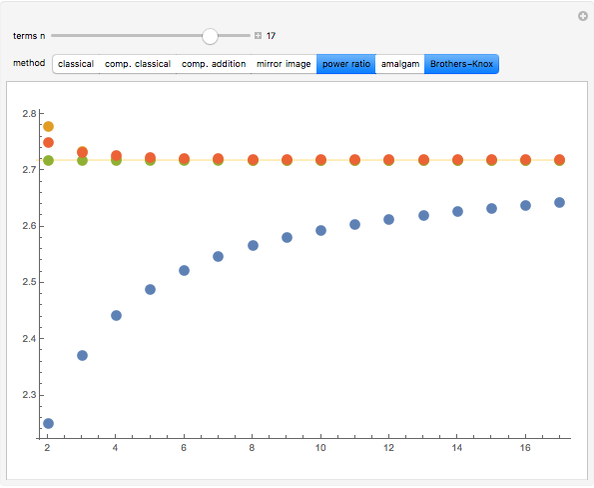
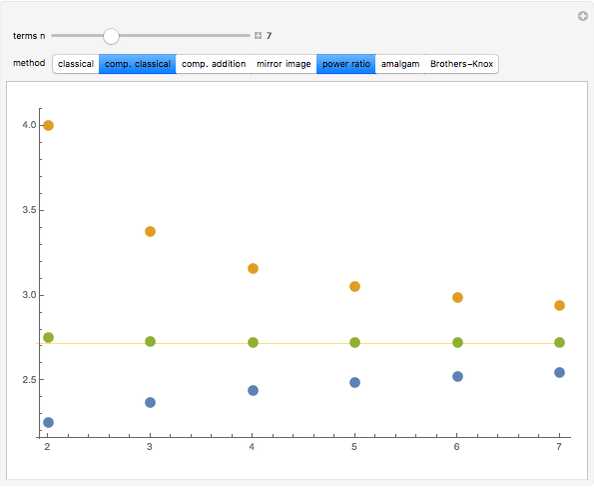
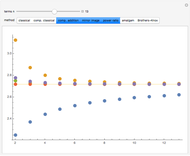
There are many different closed-form expressions for Euler's number . All are functions such that approaches as approaches infinity. However, each expression exhibits a different rate of convergence. This Demonstration offers a visual representation of the behavior of these functions at smaller values of .

Contributed by: Sakethnath Are (January 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Methods

classical:

complementary classical:

complementary addition (CAM):

mirror image (MIM):

power ratio (PRM):

CAM-MIM-PRM amalgam:

Brothers–Knox:

Reference

[1] H. J. Brothers and J. A. Knox, "New Closed-Form Approximations to the Logarithmic Constant e," The Mathematical Intelligencer, 20(4), 1998 pp. 25–29.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send