Comparing Simple Crank/Slider and Scotch Yoke Mechanisms


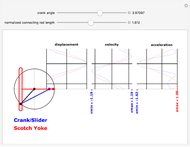
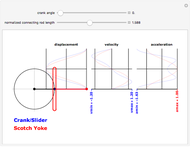
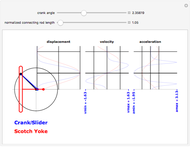
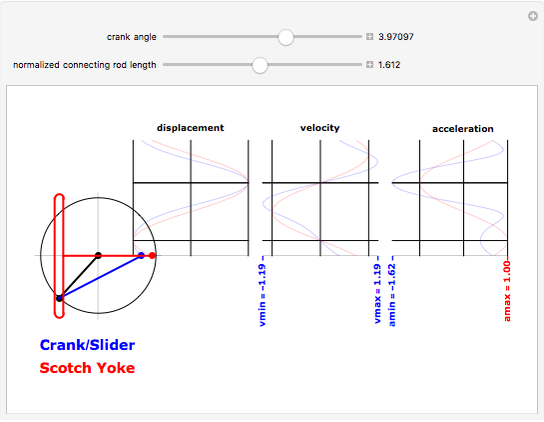
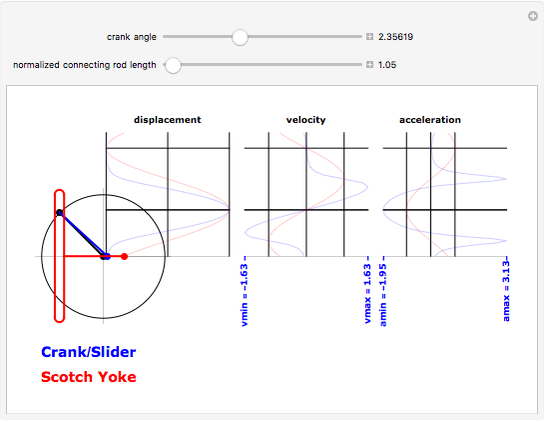
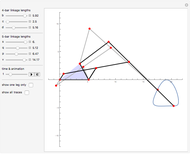
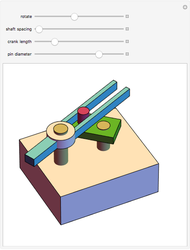
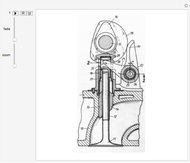
	The simple crank/slider and the Scotch yoke (called the Donkey Crosshead in Great Britain) are two mechanisms for transforming between rotary and linear motion. This Demonstration compares the sliding joint kinematics—the displacements, velocities, and accelerations—produced by the two mechanisms as functions of the common input crank angle. The mechanism schematic shows the shared crank in black, the connecting rod of the simple crank mechanism in blue, and the Scotch yoke superposed in red. The kinematics for the sliding joint are plotted for a complete cycle in corresponding colors on the strip chart. To animate the Demonstration, click on the "+" to the right of the "crank angle" slider to open playback controls.


	Contributed by: Fred Klingener

The basis for the kinematics and the graphical display is a crank length of unity, yielding a stroke of 2 for both mechanisms. The connecting rod length is normalized to the crank length. For a constant crank rotational speed of

radians per second, the Scotch yoke produces a pin displacement at time

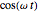, a pin velocity of

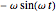, and a pin acceleration of

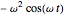. The strip chart plots are normalized to these values, independent of any manipulated value of the crank angle.

The minima and maxima are color-coded to the mechanism that produces them. Notice that for long connecting rods, the Scotch yoke produces a maximum pin acceleration (at top dead center) that is larger than that of the simple crank.

The displacement strip chart shows the relatively longer dwell time produced by the Scotch yoke at the top of the stroke, and this feature is sometimes offered as a potential advantage in the design of an internal combustion engine.