Gibbs Phenomena for 1D Fourier Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
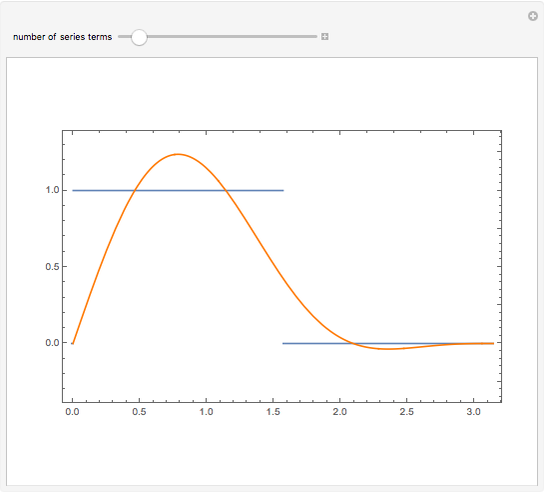
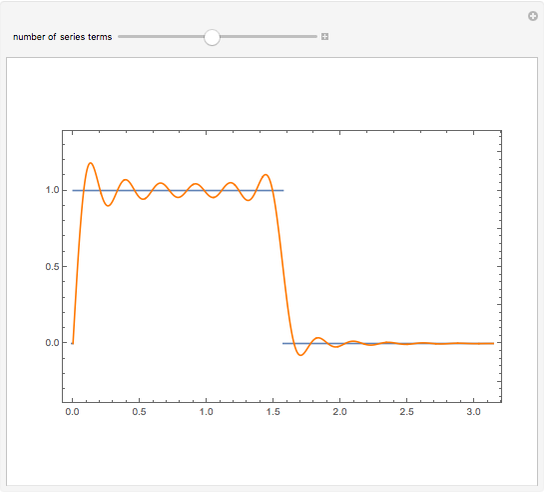
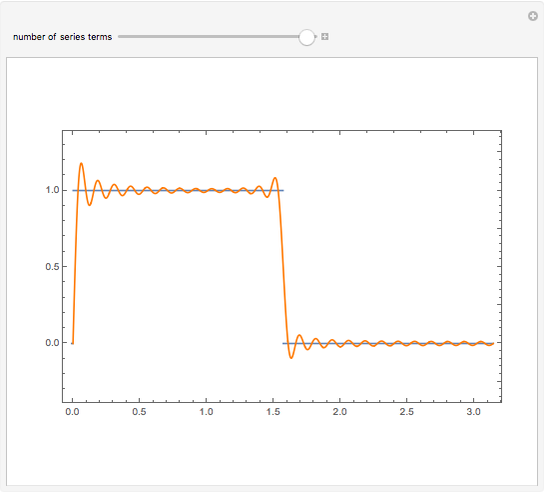
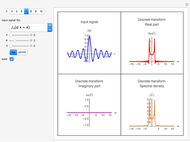
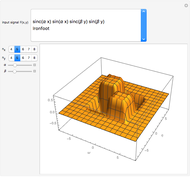
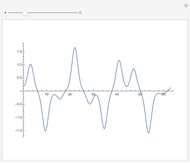
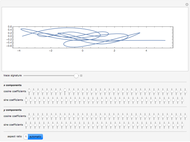
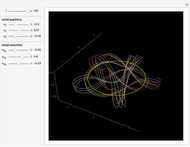
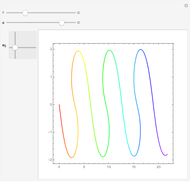
The pointwise limit of the Fourier series of a function with discontinuities does not converge pointwise to the original function everywhere.
Contributed by: Michael Trott (March 2011)
Open content licensed under CC BY-NC-SA
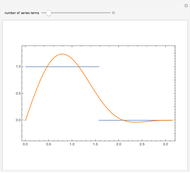
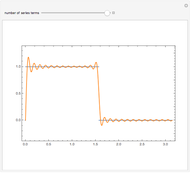
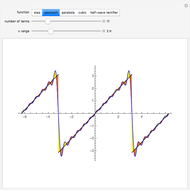
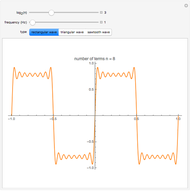
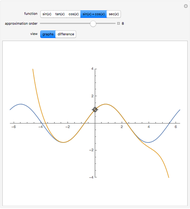
Snapshots
Details
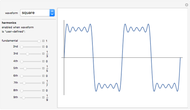
number of series terms — number of terms taken into account for the Fourier series expansion
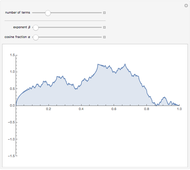
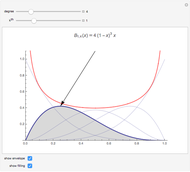
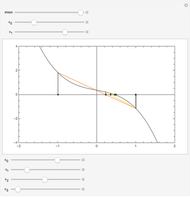
The Fourier series of a continuous, sufficiently smooth function converges pointwise to the original function. For discontinuous functions, the series converges in the  norm but does not converge pointwise. At points where the function is discontinuous, the value of the series can deviate from the original function value; at a jump discontinuity, the value of the Fourier series converges to the average of the values of the left-and right-sided limits of the original function. For truncated Fourier series, the partial sums will overshoot the original function value for
norm but does not converge pointwise. At points where the function is discontinuous, the value of the series can deviate from the original function value; at a jump discontinuity, the value of the Fourier series converges to the average of the values of the left-and right-sided limits of the original function. For truncated Fourier series, the partial sums will overshoot the original function value for  values near discontinuities; this is known as the Gibbs phenomenon.
values near discontinuities; this is known as the Gibbs phenomenon.
Permanent Citation
"Gibbs Phenomena for 1D Fourier Series"
http://demonstrations.wolfram.com/GibbsPhenomenaFor1DFourierSeries/
Wolfram Demonstrations Project
Published: March 7 2011