Cosine and Sine Identities with Dihedral Transformations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
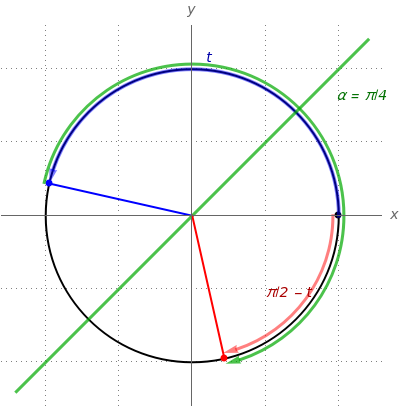
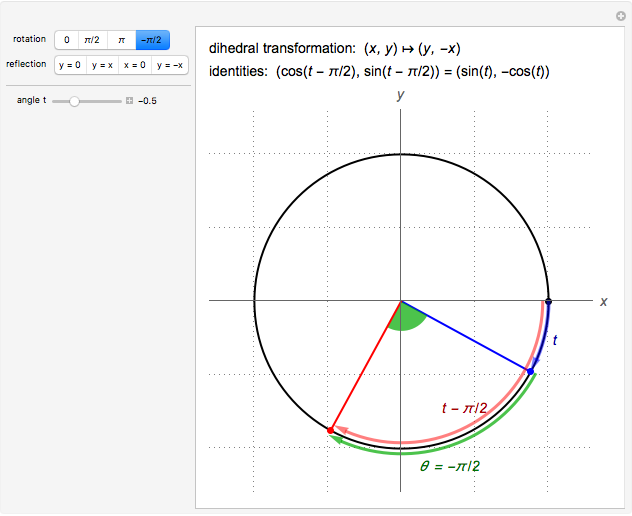
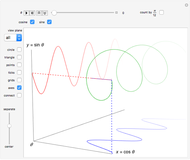
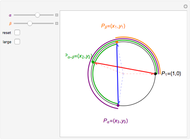
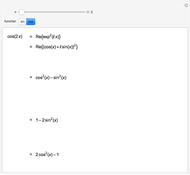
The relation between certain cosine and sine identities and certain rotations and reflections in the plane are exhibited. For example, 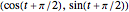 is the same as
is the same as 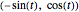 , which is the
, which is the 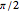 (90°) clockwise rotation,
(90°) clockwise rotation, 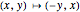 , of the point
, of the point 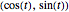 .
.
Contributed by: Gerry Harnett (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
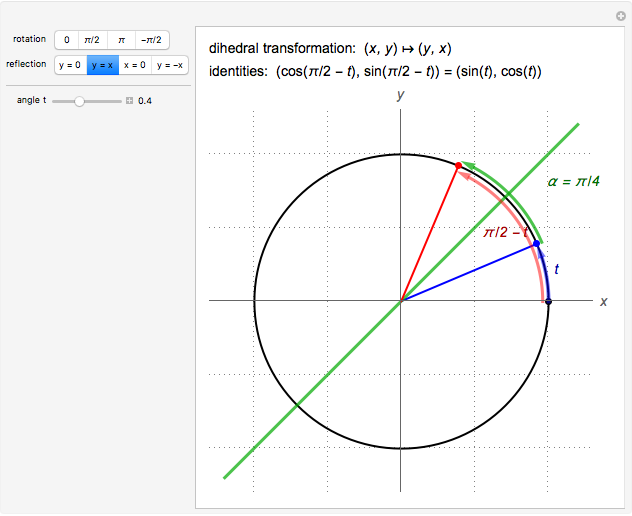
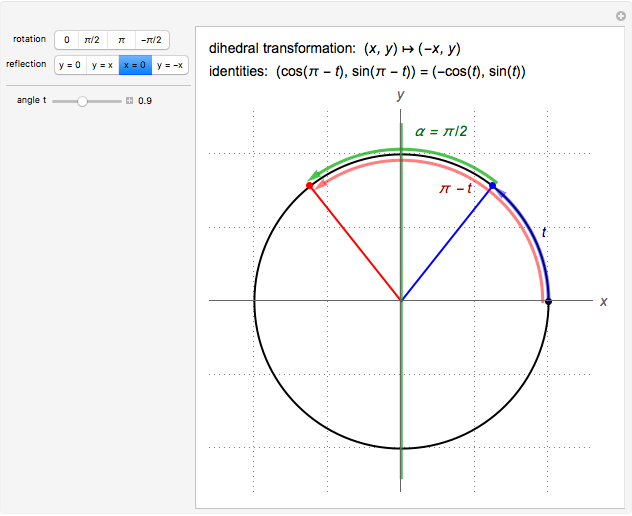
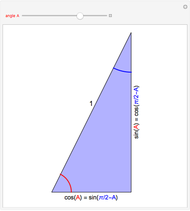
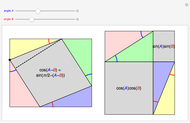
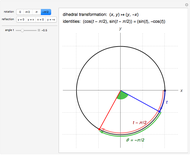
The cosine and sine angle addition identities encompass the rotation and reflection symmetries of the unit circle. Frequently noted special cases of these identities encompass what is called the dihedral group of index 4. This Demonstration exhibits the relation between these special identities and dihedral symmetries of the unit circle. A (one-dimensional) translation of  by
by 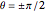 , or
, or 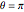 corresponds to the rotation in the plane by the angle
corresponds to the rotation in the plane by the angle  , acting on the point
, acting on the point 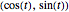 . A (one-dimensional) reflection of
. A (one-dimensional) reflection of  across
across  ,
, 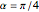 ,
, 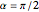 , or
, or 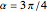 (given by
(given by 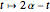 ) corresponds to the reflection in the plane across the line through the origin at angle
) corresponds to the reflection in the plane across the line through the origin at angle  (with respect to the positive
(with respect to the positive  axis), acting on the point
axis), acting on the point 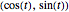 .
.
Permanent Citation