Integrating Odd Powers of Sine and Cosine by Substitution

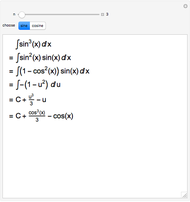
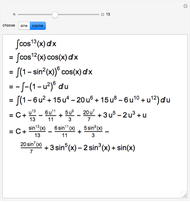
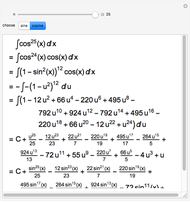
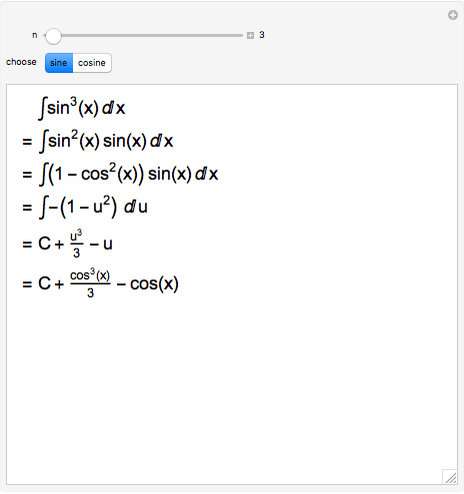
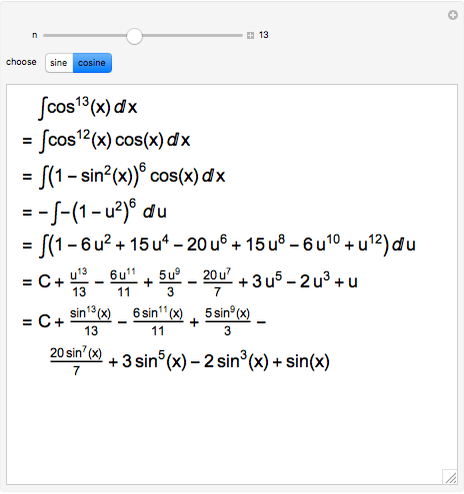
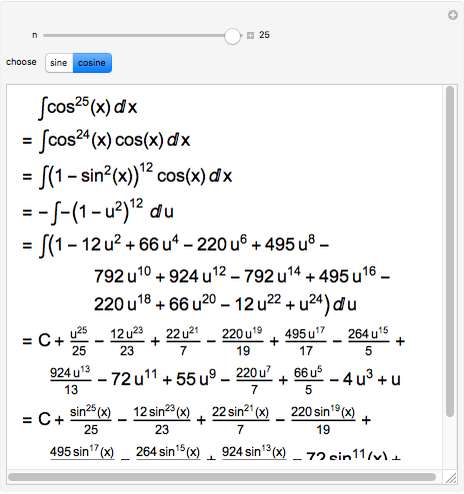
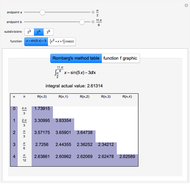
This Demonstration shows the first two steps in how to put an odd power of a sine into a form suitable for integration. Suppose the expression is .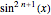
(1) split off one sine to get
(2) use 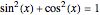to express 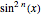in terms of
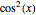(3) substitute 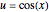, because , which absorbs the split-off sine
(4) expand the polynomial in (unless )
(5) integrate the resulting polynomial in terms of
(6) substitute back

The same technique applies to odd powers of cosines. This technique does not work for even powers of sine or cosine; in that case use a reduction formula instead.