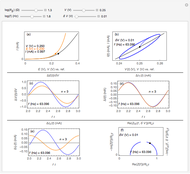
Cyclic Voltammetry for a Redox Reaction with Diffusion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
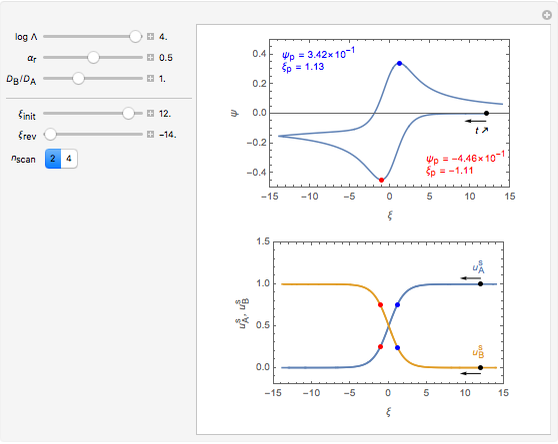
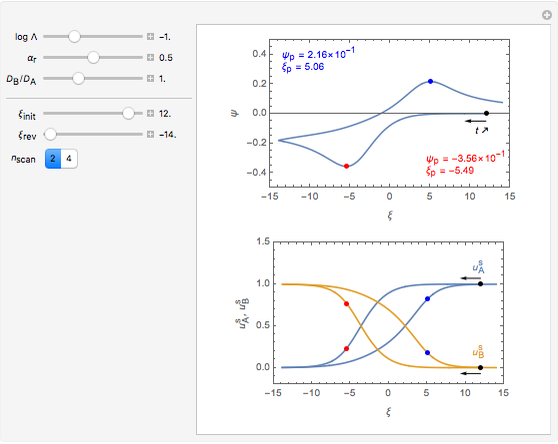
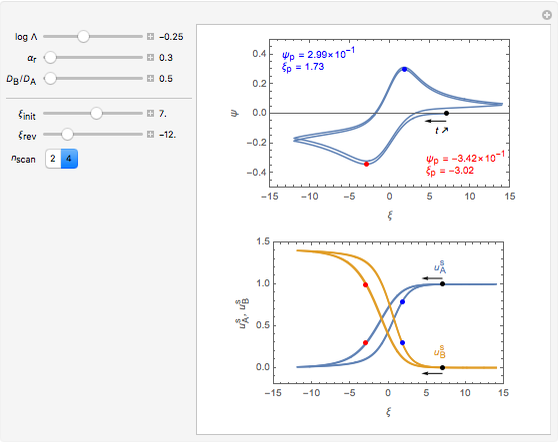
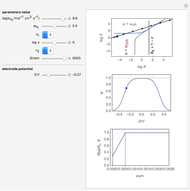
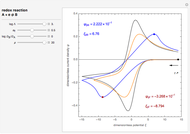
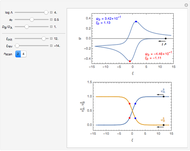
This Demonstration shows a numerical simulation of the cyclic-voltammetric response for a one-step redox reaction ( ) involving two soluble species. Mass transport of both species is characterized as 1D semi-infinite diffusion from or toward a planar electrode in a quiescent electrolyte. Cyclic voltammogram and interfacial concentration versus potential curves are plotted. You can experiment with the effects of electron transfer kinetics, mass transport, and potential scan rate using the controls for the dimensionless parameters. You can also explore the dependence on initial and reversal potentials,
) involving two soluble species. Mass transport of both species is characterized as 1D semi-infinite diffusion from or toward a planar electrode in a quiescent electrolyte. Cyclic voltammogram and interfacial concentration versus potential curves are plotted. You can experiment with the effects of electron transfer kinetics, mass transport, and potential scan rate using the controls for the dimensionless parameters. You can also explore the dependence on initial and reversal potentials,  and
and  .
.
Contributed by: Claude Montella and Jean-Paul Diard (February 2016)
(Univ. Grenoble Alpes, LEPMI, Grenoble, France)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration models the Faradaic response for a one-step redox reaction ( ) to a typical cyclic-voltammetry (CV) input signal. The reaction involves two soluble species,
) to a typical cyclic-voltammetry (CV) input signal. The reaction involves two soluble species,  and
and  , on a planar electrode (e.g., Pt electrode) in a quiescent electrolyte.
, on a planar electrode (e.g., Pt electrode) in a quiescent electrolyte.
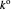 Dimensionless notation is used for the sake of generality. The relevant notation is
Dimensionless notation is used for the sake of generality. The relevant notation is  ,
, 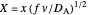 ,
, 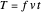 ,
, 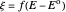 , and
, and 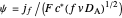 , where
, where 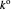 InlineMath denotes the standard rate constant (cm/s) for electron transfer at the electrolyte/electrode interface,
InlineMath denotes the standard rate constant (cm/s) for electron transfer at the electrolyte/electrode interface, 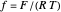 , all symbols having their usual meaning,
, all symbols having their usual meaning,  is the symmetry factor for electron transfer in the reduction direction (here forward direction),
is the symmetry factor for electron transfer in the reduction direction (here forward direction),  is the potential scan rate in V/s,
is the potential scan rate in V/s,  is the diffusion coefficient for species
is the diffusion coefficient for species 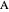 in
in  /s,
/s, 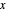 is the distance from the electrode surface in cm,
is the distance from the electrode surface in cm,  is the time variable in s,
is the time variable in s, 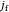 is the Faradaic current density in A/
is the Faradaic current density in A/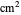 ,
, 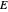 is the controlled potential (with linear variation with respect to time), and
is the controlled potential (with linear variation with respect to time), and 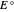 is the formal potential of redox couple, both potentials being given in V versus the reference electrode. Setting
is the formal potential of redox couple, both potentials being given in V versus the reference electrode. Setting  , for example, the dimensionless input signal is
, for example, the dimensionless input signal is 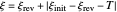 with
with 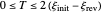 , where
, where  and
and 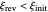 are the dimensionless initial and reversal potentials, respectively. The initial potential is taken as the equilibrium potential of the electrode pertaining to the bulk concentrations
are the dimensionless initial and reversal potentials, respectively. The initial potential is taken as the equilibrium potential of the electrode pertaining to the bulk concentrations 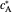 and
and 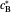 such as
such as  in
in 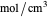 , so the initial and bulk concentrations for species
, so the initial and bulk concentrations for species 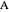 and
and 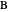 are equal to
are equal to 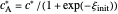 and
and 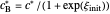 , respectively.
, respectively.
The numerical solution of the 1D linear diffusion equations, together with the boundary condition (relative to electrochemical kinetics) at the electrolyte/electrode interface and the bulk conditions (constant concentrations with respect to time), is readily obtained using the so-called method of lines implemented in Mathematica's built-in function NDSolve. The dimensionless current density 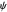 is computed versus time from the dimensionless flux of electroactive species at the interface. You can vary the parameters
is computed versus time from the dimensionless flux of electroactive species at the interface. You can vary the parameters 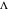 (logarithmic scale) and
(logarithmic scale) and 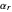 as well as the diffusion coefficient ratio
as well as the diffusion coefficient ratio 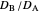 . You can also vary the dimensionless initial potential
. You can also vary the dimensionless initial potential  and reversal potential
and reversal potential  within some limits.
within some limits.
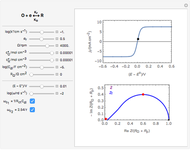
Numerical simulation provides the dimensionless cyclic voltammogram (the parametric curve 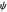 versus
versus  ), together with the dimensionless concentration of redox species,
), together with the dimensionless concentration of redox species, 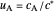 and
and 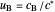 , as a function of dimensionless space and time variables. The interfacial values (
, as a function of dimensionless space and time variables. The interfacial values (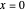 , with superscript "s"), that satisfy
, with superscript "s"), that satisfy  with
with 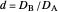 , are plotted versus
, are plotted versus  .
.
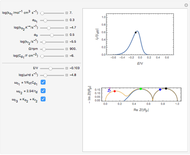
The dimensionless coordinates of CV peaks are evaluated in both the reduction (forward scan) and oxidation (reverse scan) directions, whenever such peaks exist. The two limiting behaviors (relative to the first forward scan only) pertaining respectively to reversible electron-transfer kinetics (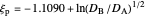 and
and  , observed at large enough values of
, observed at large enough values of 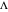 and
and 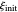 , irrespective of
, irrespective of 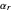 ) and totally irreversible kinetics (
) and totally irreversible kinetics (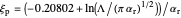 and
and 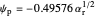 , observed at low enough values of
, observed at low enough values of 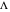 and large enough values of
and large enough values of 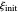 , irrespective of
, irrespective of 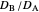 ) can be readily obtained from numerical experimentation.
) can be readily obtained from numerical experimentation.
References
[1] A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, 2nd ed., New York: Wiley, 2001.
[2] J.-P. Diard, B. Le Gorrec, and C. Montella, Cinétique électrochimique, Paris: Hermann, 1996.
[3] J. M. Savéant, Elements of Molecular and Biomolecular Electrochemistry, Hoboken, NJ: Wiley-Interscience, 2006.
Permanent Citation