Definitions of Hill's Tetrahedra

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration gives definitions of Hill's tetrahedra.
Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA
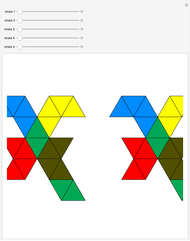
Snapshots
Details
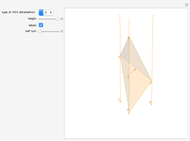
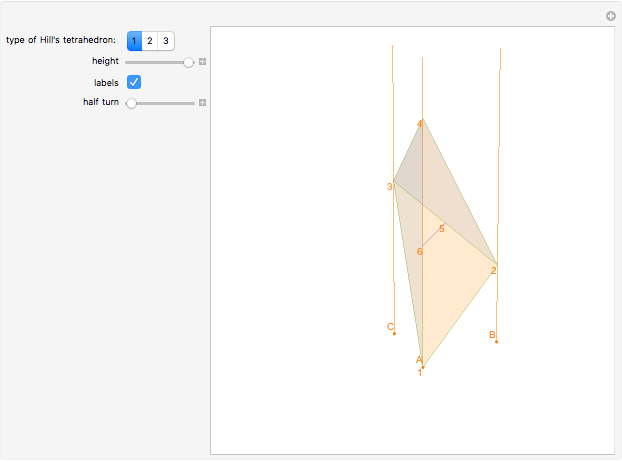
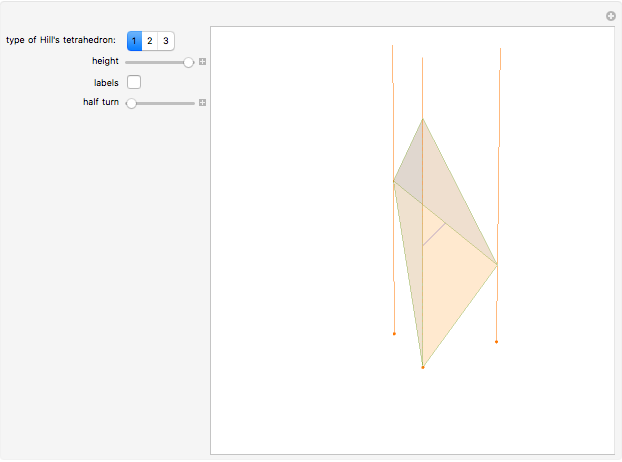
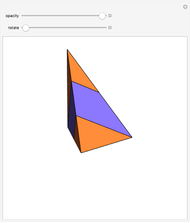
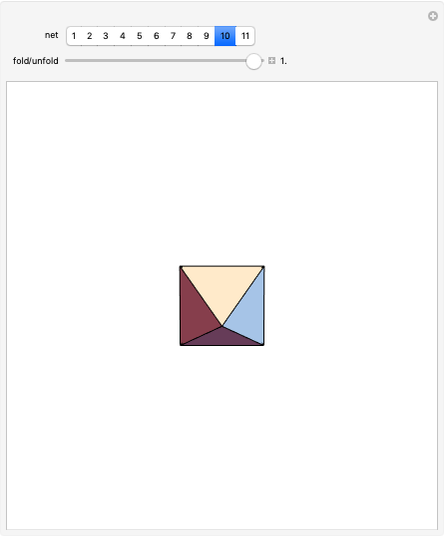
Let ABC be an equilateral triangle and let the red lines be normals to the plane of the triangle. Let 1, 2, 3, and 4 be points on the normals at heights  ,
,  ,
,  ,
, 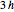 . Then the tetrahedron with vertices 1, 2, 3, 4 is Hill's tetrahedron of type 1.
. Then the tetrahedron with vertices 1, 2, 3, 4 is Hill's tetrahedron of type 1.
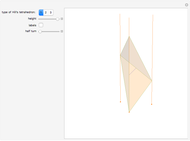
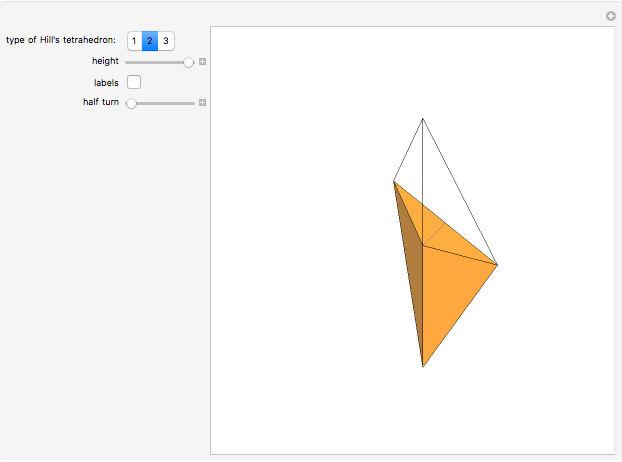
Let the points 5 and 6 be the midpoints of the segments 23 and 14. Then the straight line 56 is the axis of symmetry of the tetrahedron.
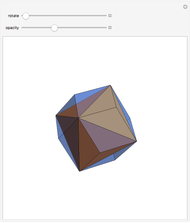
The tetrahedron with vertices 1, 2, 3, 6 is Hill's tetrahedron of type 2. Hill's tetrahedron of type 1 consists of two congruent Hill's tetrahedra of type 2.
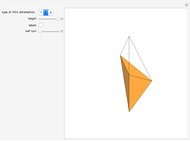
The tetrahedron with vertices 1, 2, 4, 5 is Hill's tetrahedron of type 3. Hill's tetrahedron of type 1 consists of two congruent Hill's tetrahedra of type 3.
V. G. Boltyanskii, Tretja Problema Hilberta, Moscow: Nauka, 1977. Translated by R. A. Silverman as Hilbert's Third Problem (New York: John Wiley & Sons, Inc., 1978).
Permanent Citation
"Definitions of Hill's Tetrahedra"
http://demonstrations.wolfram.com/DefinitionsOfHillsTetrahedra/
Wolfram Demonstrations Project
Published: March 7 2011