Leaking Bucket Equation and Reversibility

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
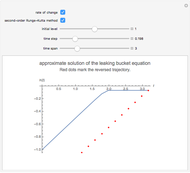
How do reversible integrators work for nonreversible differential equations, such as the leaking bucket equation? This is investigated here for the asynchronous leapfrog integrator, a presumably novel variant of the well-known leapfrog method. For comparison, one can also choose the second-order nonreversible Runge–Kutta method, which is also known as Heun's method.
[more]
Contributed by: Ulrich Mutze (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The leaking bucket equation for the water level 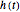 is
is  , where
, where  is the unit step function. The solution is easily seen to be
is the unit step function. The solution is easily seen to be  and says that
and says that  is zero for
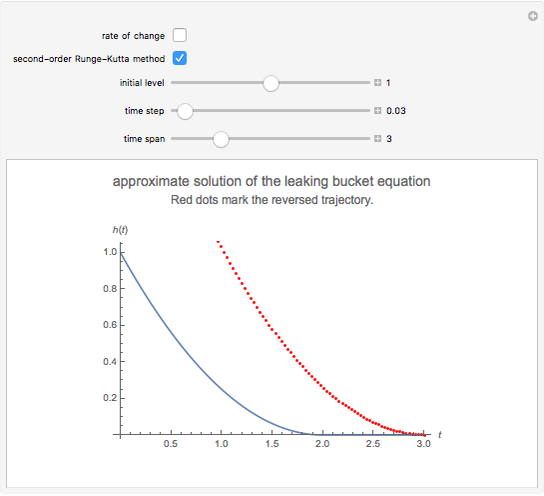
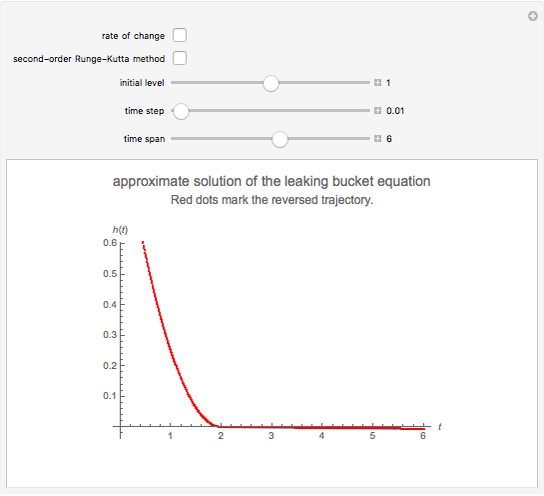
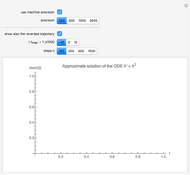
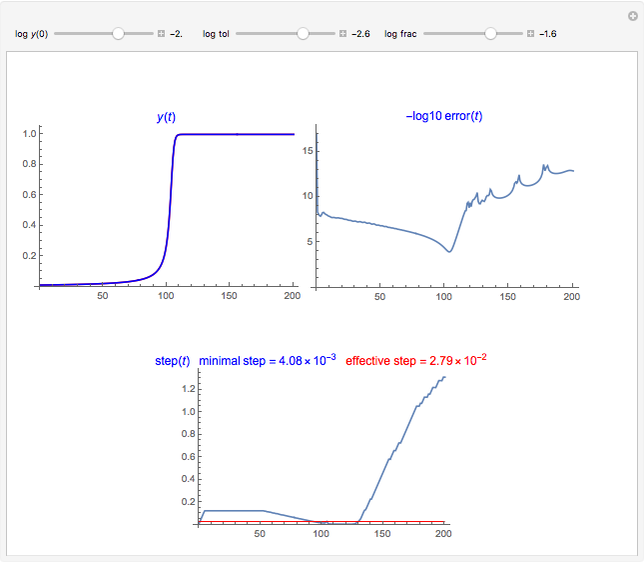
is zero for 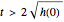 (because the bucket is empty then). In this Demonstration, we replace the exact solution by a numerical one, which is obtained by repeated application of a so-called integrator (actually the asynchronous leapfrog integrator) to the initial state of the system. We compute this solution well beyond the time
(because the bucket is empty then). In this Demonstration, we replace the exact solution by a numerical one, which is obtained by repeated application of a so-called integrator (actually the asynchronous leapfrog integrator) to the initial state of the system. We compute this solution well beyond the time 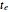 that the bucket is empty. Because the integrator under consideration is reversible, we can take the final (empty) state and evolve it back in exact agreement with the forward evolution. Along this reversed trajectory, the bucket will start to get filled exactly at time
that the bucket is empty. Because the integrator under consideration is reversible, we can take the final (empty) state and evolve it back in exact agreement with the forward evolution. Along this reversed trajectory, the bucket will start to get filled exactly at time 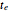 . How can this be? It works because the state description according to the asynchronous leapfrog method contains, in addition to the water level, a second quantity. In most cases this quantity behaves like
. How can this be? It works because the state description according to the asynchronous leapfrog method contains, in addition to the water level, a second quantity. In most cases this quantity behaves like 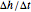 . However, when
. However, when  approaches the value 0 on a trajectory of the leaking bucket equation, the steepness of the right-hand side of this equation makes this second quantity oscillate. It is only the mean value over two consecutive steps that resembles
approaches the value 0 on a trajectory of the leaking bucket equation, the steepness of the right-hand side of this equation makes this second quantity oscillate. It is only the mean value over two consecutive steps that resembles 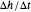 . This oscillation together with a small linear trend of
. This oscillation together with a small linear trend of  carries the information concerning the moment of emptying.
carries the information concerning the moment of emptying.
References:
[1] U. Mutze, "An Asynchronous Leap-Frog Method".
Permanent Citation
"Leaking Bucket Equation and Reversibility"
http://demonstrations.wolfram.com/LeakingBucketEquationAndReversibility/
Wolfram Demonstrations Project
Published: March 7 2011