Differential Equation with a Discontinuous Forcing Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
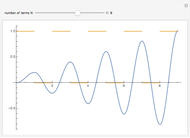
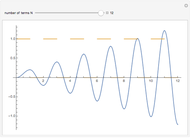
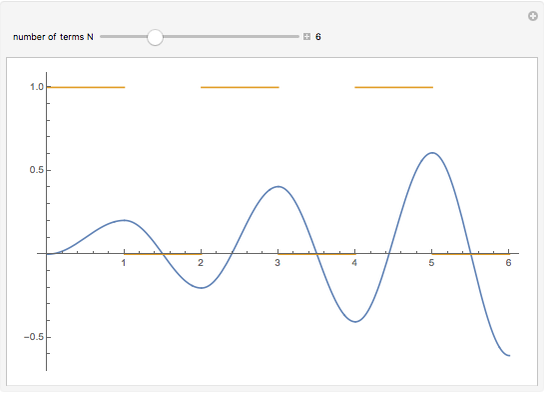
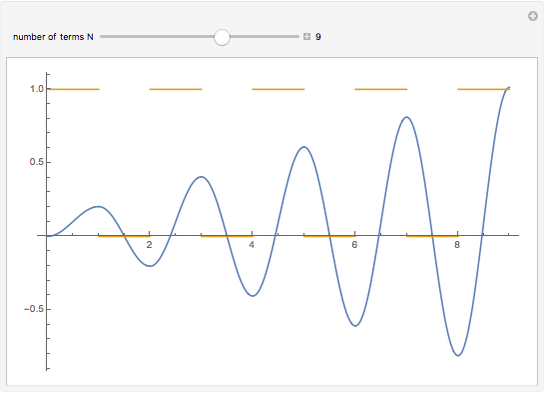
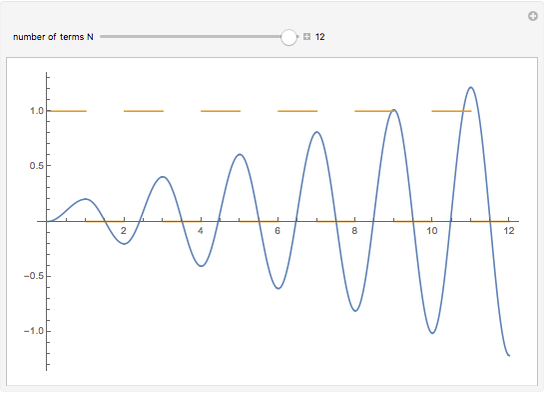
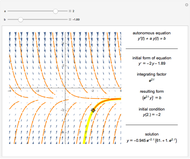
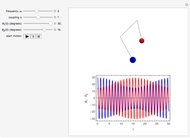
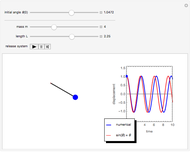
Consider the equation  , where
, where  is a square-wave step function and
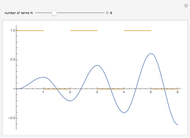
is a square-wave step function and  is the oscillation of a spring-mass system in resonance with the square-wave forcing function. The graph of
is the oscillation of a spring-mass system in resonance with the square-wave forcing function. The graph of 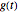 is drawn in purple and that of
is drawn in purple and that of 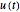 in blue. Using Laplace transforms, this solution is more compact than using a Fourier series expansion of the forcing function.
in blue. Using Laplace transforms, this solution is more compact than using a Fourier series expansion of the forcing function.
Contributed by: Stephen Wilkerson (March 2011)
(United States Military Academy West Point, Department of Mathematics)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This example comes from [1], Section 5.6, Differential Equations with Discontinuous Forcing Functions.
Reference
[1] J. R. Brannan and W. E. Boyce, Differential Equations with Boundary Value Problems: An Introduction to Modern Methods and Applications, New York: John Wiley and Sons, 2010.
Permanent Citation