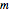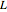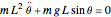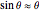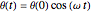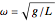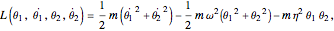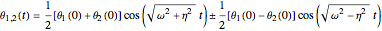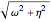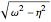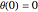Dynamics of Coupled Pendulums

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
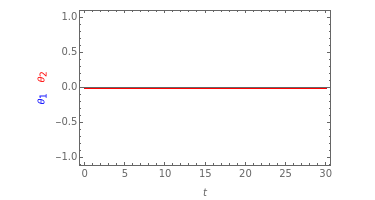
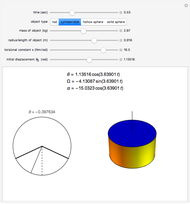
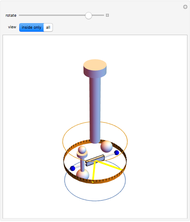
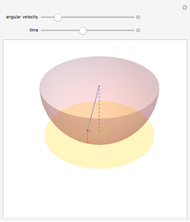
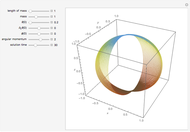
Consider a system of two identical pendulums swinging in parallel planes and connected at the top by a flexible string. (A recently published Demonstration considered the related version of two pendulums with their bobs connected by a massless spring.) We describe here a more classic form of the problem, going back to the time of Huygens.
[more]
Contributed by: S. M. Blinder (August 2009)
After work by: Stephen Wilkerson
Open content licensed under CC BY-NC-SA
Snapshots
Details
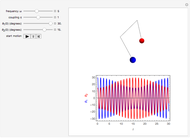
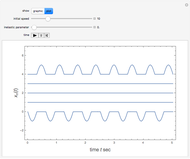
Snapshot 1: in-phase normal mode, starting with 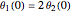
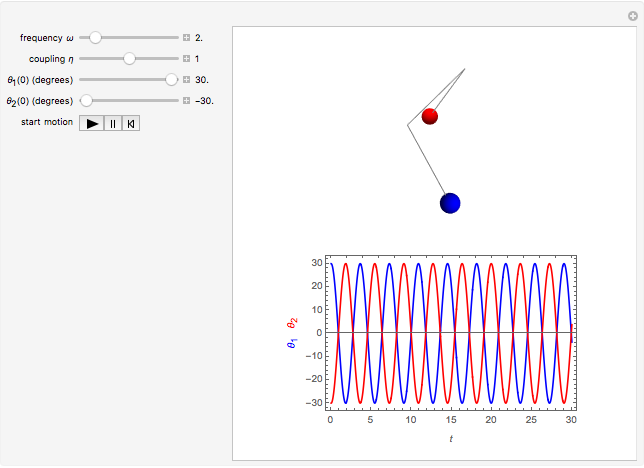
Snapshot 2: out-of phase normal mode
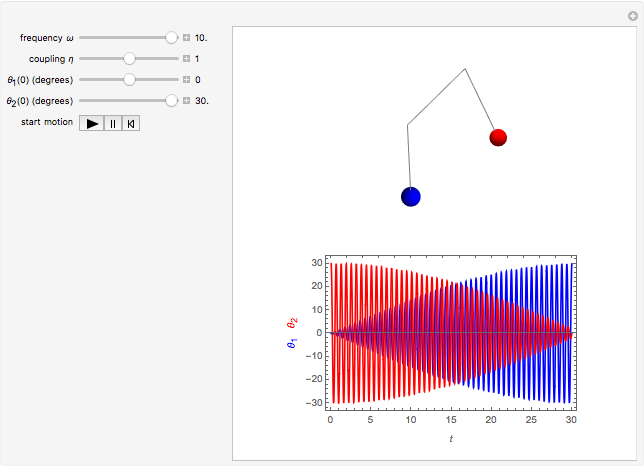
Snapshot 3: two pendulums showing resonant exchange of energy
See this YouTube video for a real-life visualization of this Demonstration.
Permanent Citation