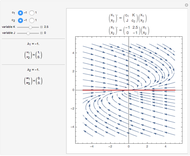
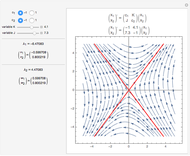
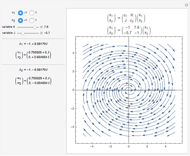
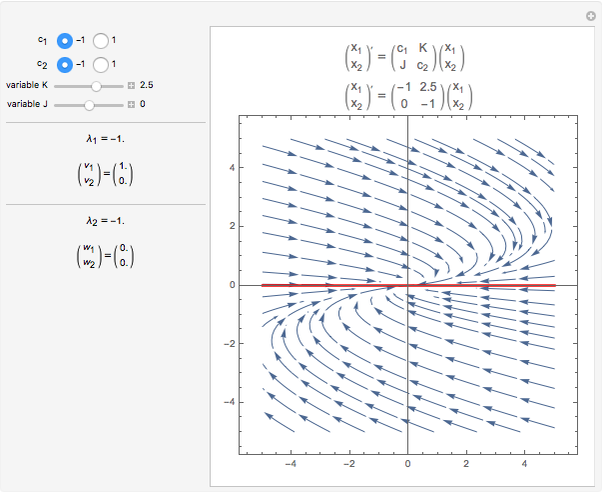
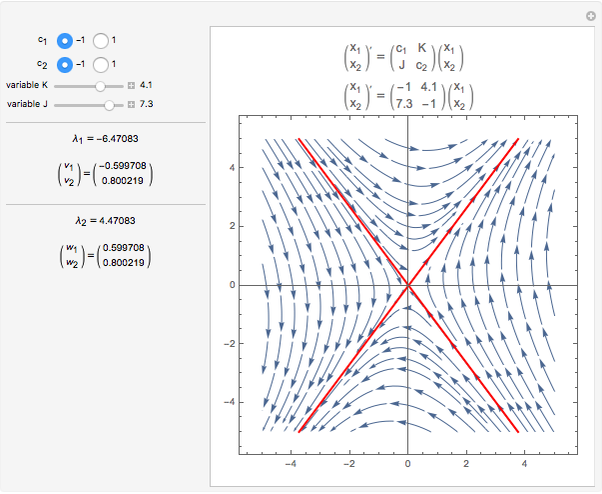
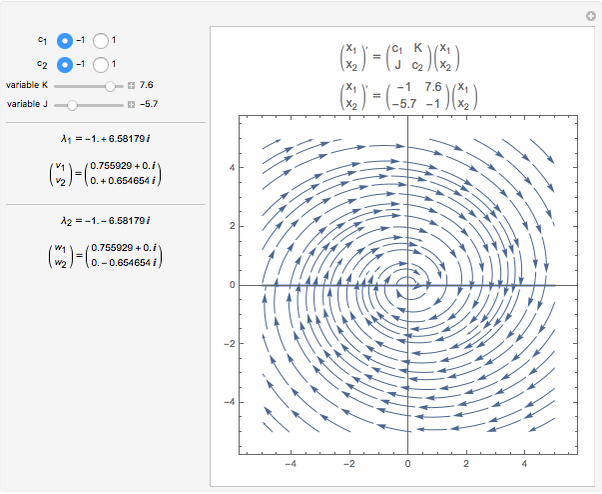
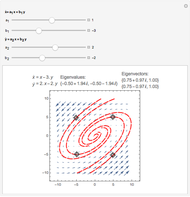
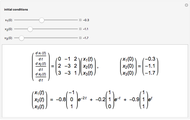
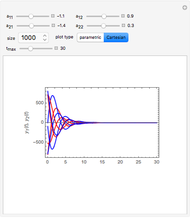
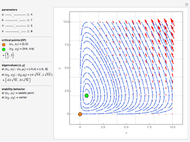
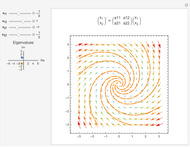
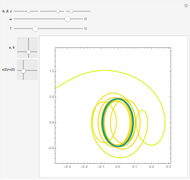
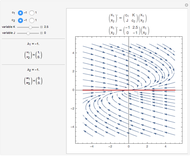
This Demonstration plots an extended phase portrait for a system of two first-order homogeneous coupled equations and shows the eigenvalues and eigenvectors for the resulting system. You can vary any of the variables in the matrix to generate the solutions for stable and unstable systems. The eigenvectors are displayed both graphically and numerically. The following phenomena can be seen: stable and unstable saddle points, lines of equilibria, nodes, improper nodes, spiral points, sinks, nodal sinks, spiral sinks, saddles, sources, spiral sources, nodal sources, and centers.