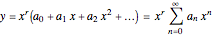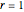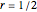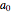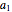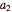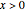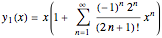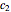Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Series Solution of a Cauchy-Euler Equation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

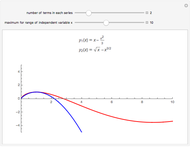
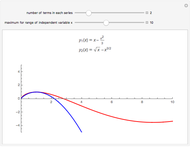
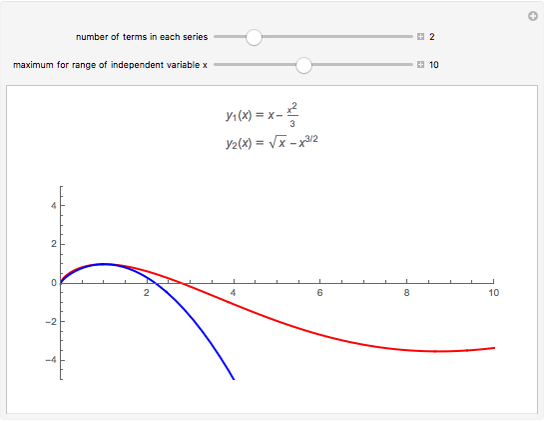
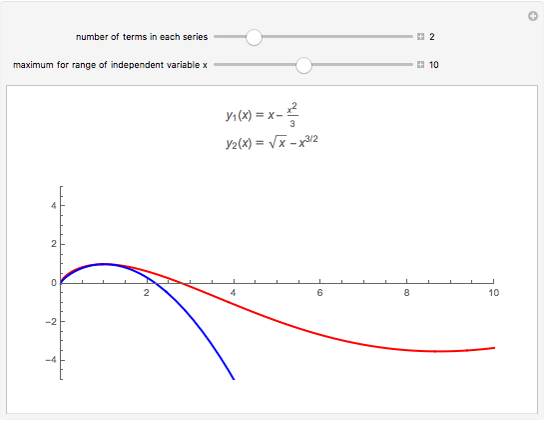
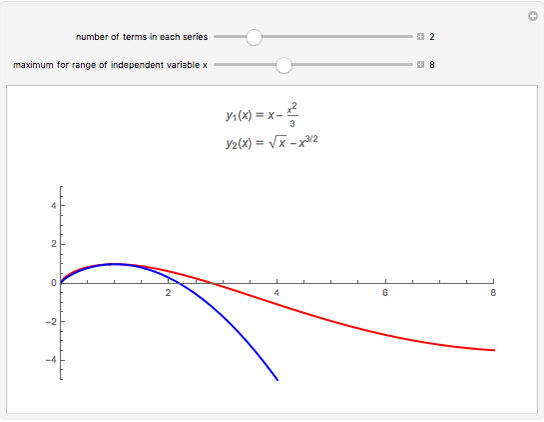
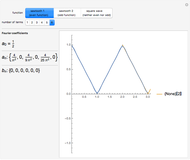
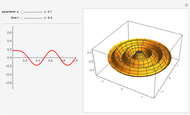
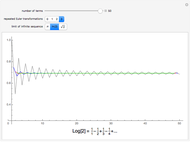
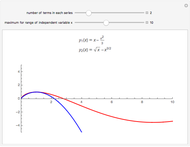
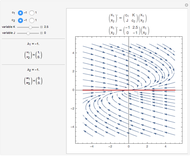
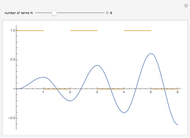
This Demonstration shows the solution to the Cauchy–Euler equation with initial conditions 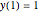and 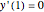and approximations to it using truncated series.

[more]

Assume solutions have the form

.

Take the first and second derivatives of this equation and substitute back into the original equation. If the equation is to be satisfied for all , the coefficient of each power of must be zero. This gives a quadratic equation in with roots and . Then the coefficients , , , … can be determined. The two solutions for are:

,

.

The final solution (plotted in blue) has the form , where and are determined by the initial conditions. With not too many terms it serves as a good approximation to the exact solution (plotted in red).

[less]

Contributed by: Stephen Wilkerson (December 2010)
(United States Military Academy West Point, Department of Mathematics)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This example comes from Chapter 8 of [1] on series solutions and the Cauchy–Euler equation.

Reference

[1] J. R. Brannan and W. E. Boyce, Differential Equations with Boundary Value Problems: An Introduction to Modern Methods and Applications, New York: John Wiley and Sons, 2010.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send