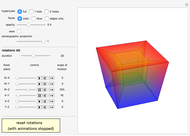
Dihedral Group of the Square

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
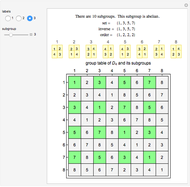
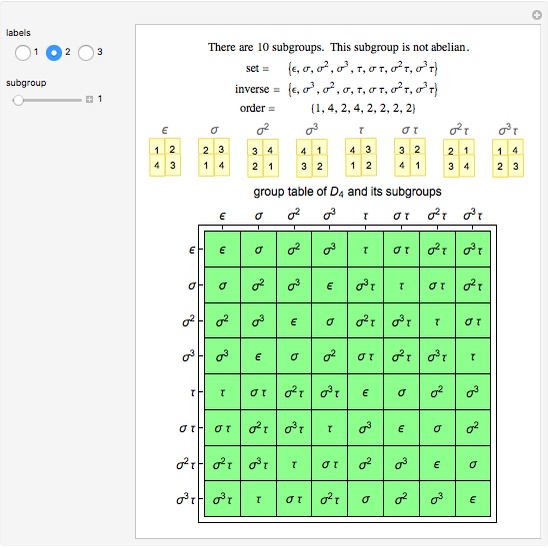
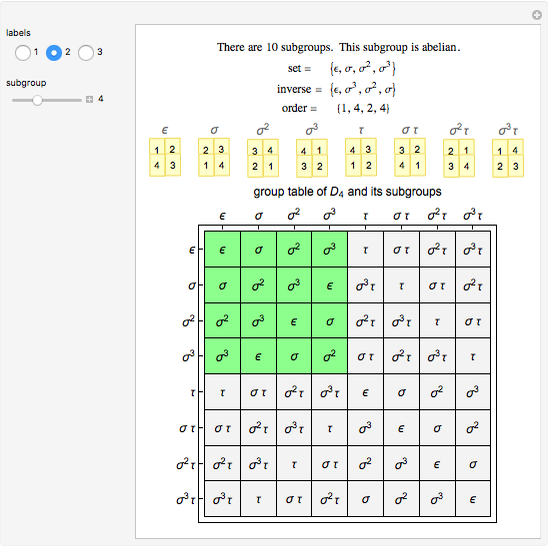
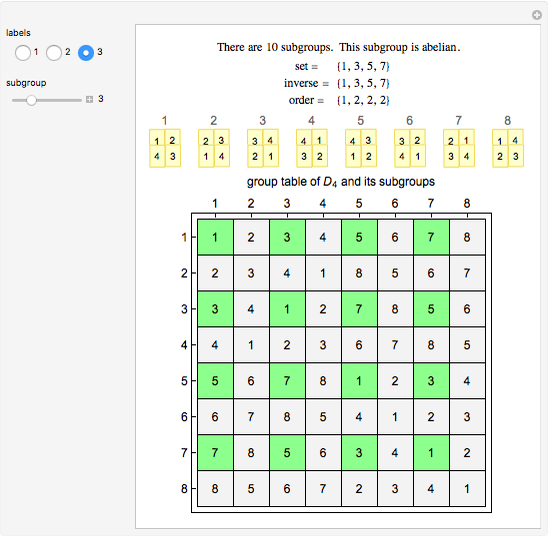
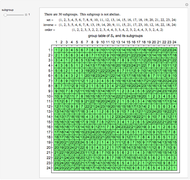
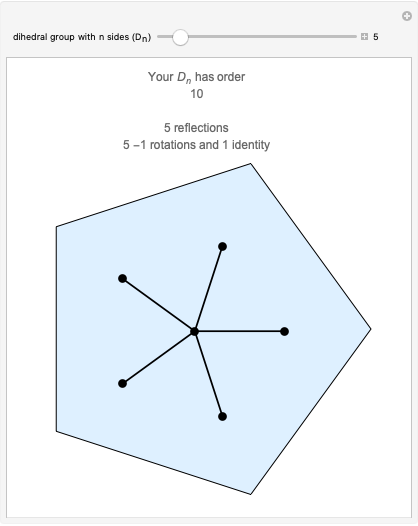
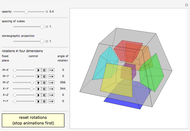
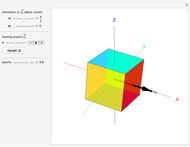
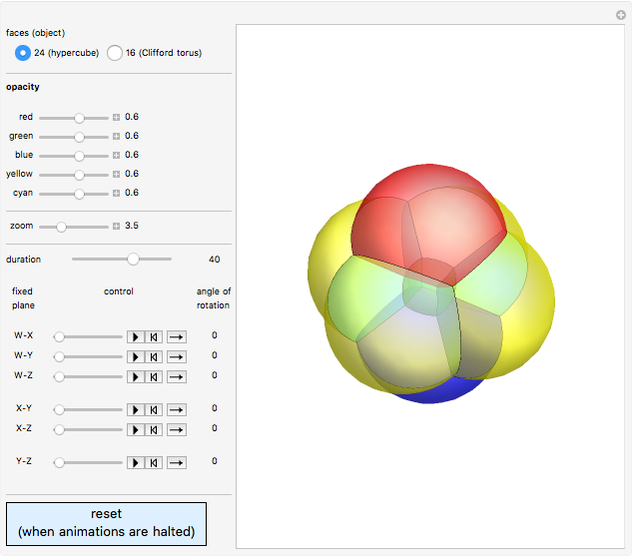
In mathematics, a dihedral group 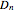 is the group of symmetries of a regular polygon with
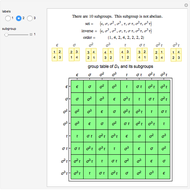
is the group of symmetries of a regular polygon with  sides, including both rotations and reflections. This Demonstration shows the subgroups of
sides, including both rotations and reflections. This Demonstration shows the subgroups of 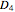 , the dihedral group of a square.
, the dihedral group of a square.
Contributed by: Gerard Balmens (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A group is a set 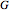 together with a binary operation
together with a binary operation  on
on 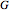 , i.e., a function
, i.e., a function  to
to 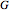 (called the group law of
(called the group law of 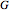 ) that combines any two elements
) that combines any two elements  and
and  to form another element, denoted
to form another element, denoted  or
or 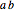 . To qualify as a group, the set and operation, (
. To qualify as a group, the set and operation, (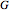 ,
,  ), must satisfy four requirements known as the group axioms: closure, associativity, identity element, and inverse element. If
), must satisfy four requirements known as the group axioms: closure, associativity, identity element, and inverse element. If 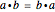 , then the group is commutative or Abelian.
, then the group is commutative or Abelian.
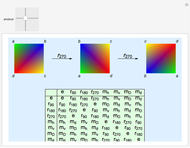
In this Demonstration, the group law is the composition of permutations of the set 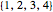 . For example,
. For example,  .
.
Permanent Citation