Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

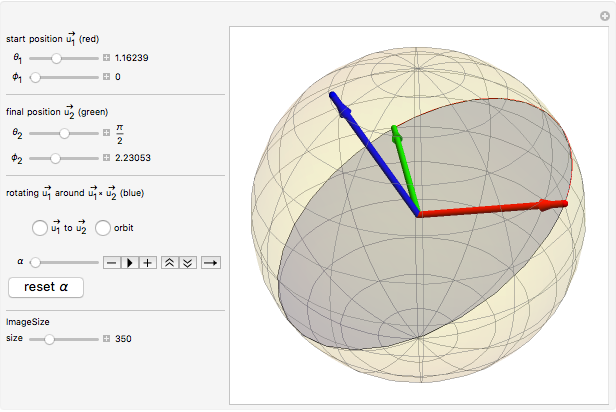
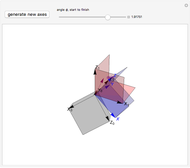
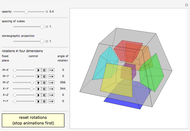
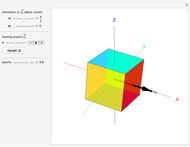
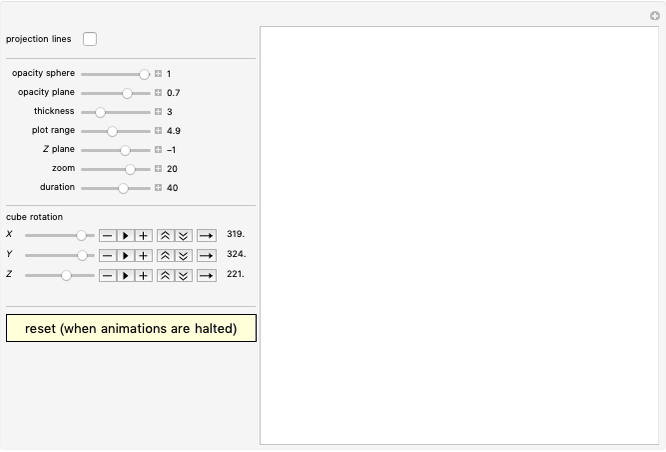
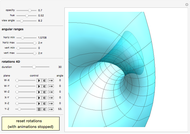
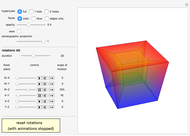
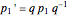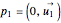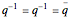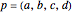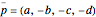Rotating a Unit Vector in 3D Using Quaternions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

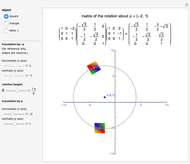
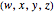A quaternion is a vector in with a noncommutative product (see [1] or Quaternion (Wolfram MathWorld)). Quaternions, also called hypercomplex numbers, were invented by William Rowan Hamilton in 1843. A quaternion can be written or, more compactly, or 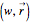, where the noncommuting unit quaternions obey the relations .

[more]

A quaternion can represent a rotation axis, as well as a rotation about that axis. Instead of turning an object through a series of successive rotations using rotation matrices, quaternions can directly rotate an object around an arbitrary axis (here ) and at any angle . This Demonstration uses the quaternion rotation formula with , a pure quaternion (with real part zero), , normalized axis , and for a unit quaternion, , where the quaternion conjugate for is .

[less]

Contributed by: Gerard Balmens (February 2016)
Open content licensed under CC BY-NC-SA

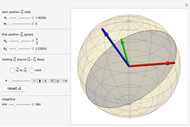
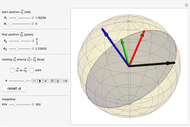
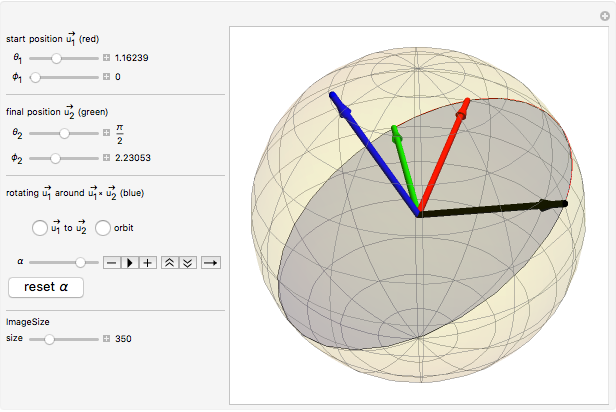
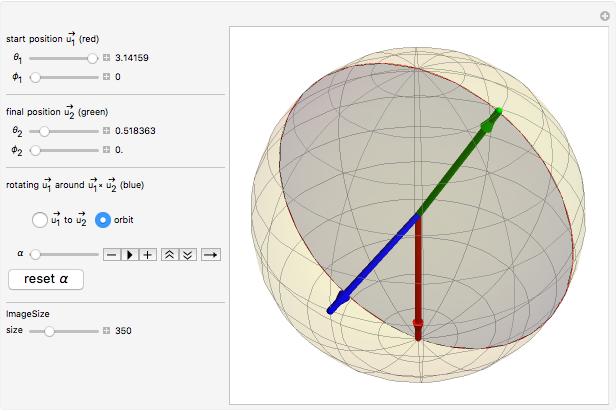
Snapshots

Details

Reference

[1] Wikipedia. "Quaternions and Spatial Rotation." (Feb 9, 2016) en.wikipedia.org/wiki/Quaternions_and_spatial _rotation.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send