Doug-all Theorem II: Inscribed Triangles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
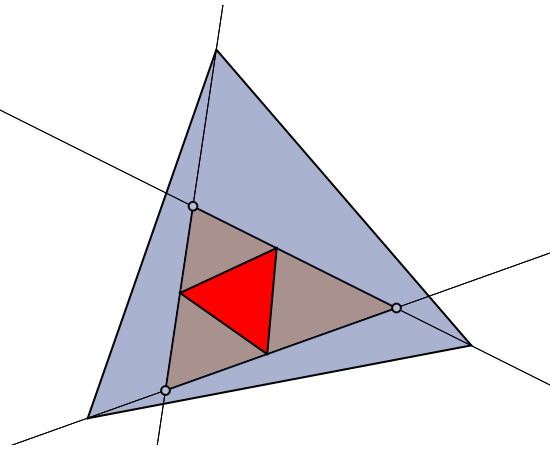
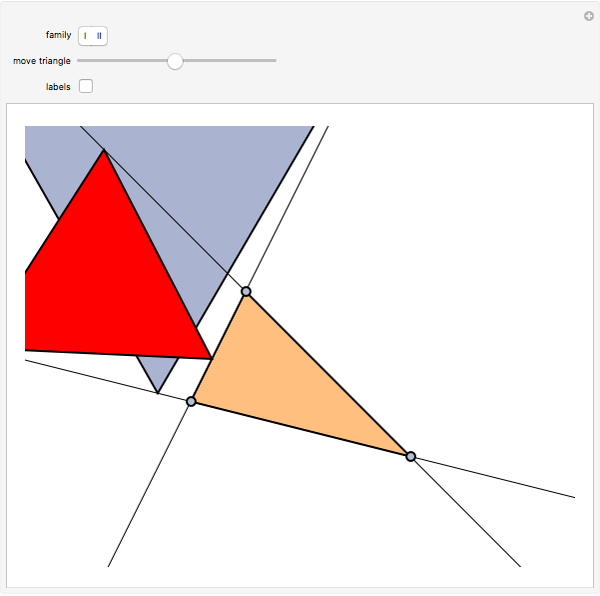
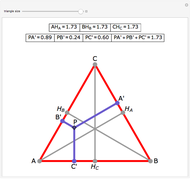
Consider the set of all equilateral triangles  inscribed about an arbitrary triangle
inscribed about an arbitrary triangle  ; that is, side
; that is, side  contains
contains  , side
, side 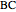 contains
contains  , and side
, and side  contains
contains  . By "side" we mean the full line, not just the line segment, so that, for instance, point
. By "side" we mean the full line, not just the line segment, so that, for instance, point  is not necessarily in between
is not necessarily in between  and
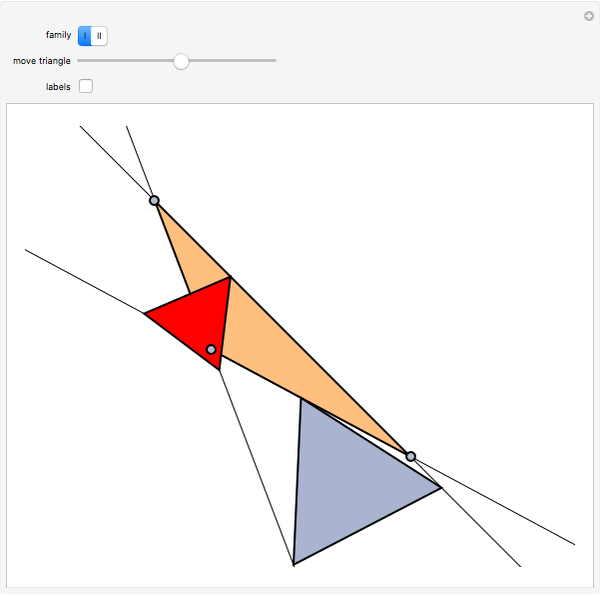
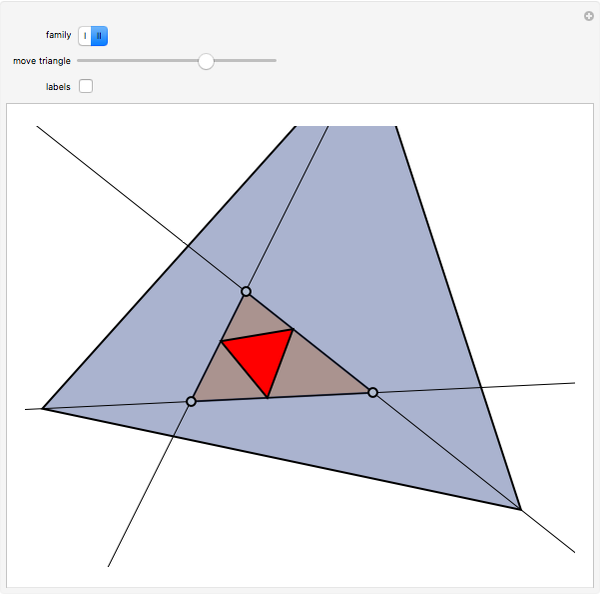
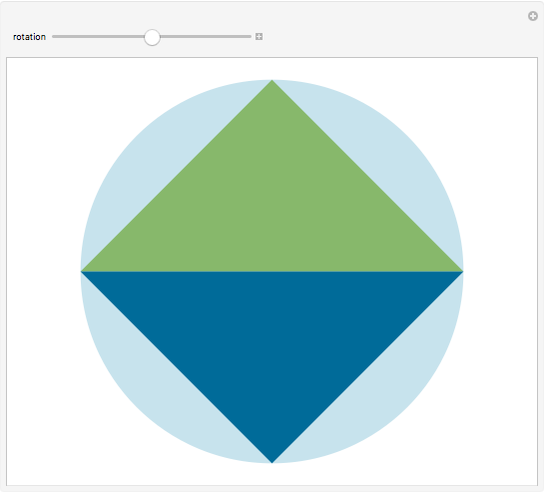
and 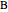 . The Doug-all theorem (its author is not to be confused with the prestigious geometer John Dougall, who died in 1960) claims that there are infinitely many such inscribed triangles, and among them there is a smallest one. There are two families of triangles
. The Doug-all theorem (its author is not to be confused with the prestigious geometer John Dougall, who died in 1960) claims that there are infinitely many such inscribed triangles, and among them there is a smallest one. There are two families of triangles  , one that has triangles completely covering
, one that has triangles completely covering  and one never covering
and one never covering  . This Demonstration lets you experiment by dragging the vertices of the triangle or moving the inscribed equilateral triangle to verify the existence of the smallest inscribed triangle, which sometimes is outside the triangle!
. This Demonstration lets you experiment by dragging the vertices of the triangle or moving the inscribed equilateral triangle to verify the existence of the smallest inscribed triangle, which sometimes is outside the triangle!
Contributed by: Jaime Rangel-Mondragon (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
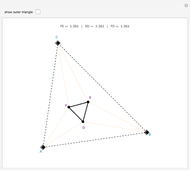
The centers of all the inscribed equilateral triangles in each family form a straight line.
Some blue triangles lie outside the window.
The character Doug-all is a fictitious character created by the distinguished writer Douglas Hofstadter.
Reference
[1] D. Hofstadter, "Napoleon's Theorem & Doug-all's Theorem (Prelude and Centrifugue in G)", in The Changing Shape of Geometry: Celebrating a Century of Geometry and Geometry Teaching (Chris Pritchard, ed.), Cambridge, UK: Cambridge University Press, 2003, pp. 265–271.
Permanent Citation
"Doug-all Theorem II: Inscribed Triangles"
http://demonstrations.wolfram.com/DougAllTheoremIIInscribedTriangles/
Wolfram Demonstrations Project
Published: August 10 2012