Drawdown Pressure in a Naturally Fractured Reservoir

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
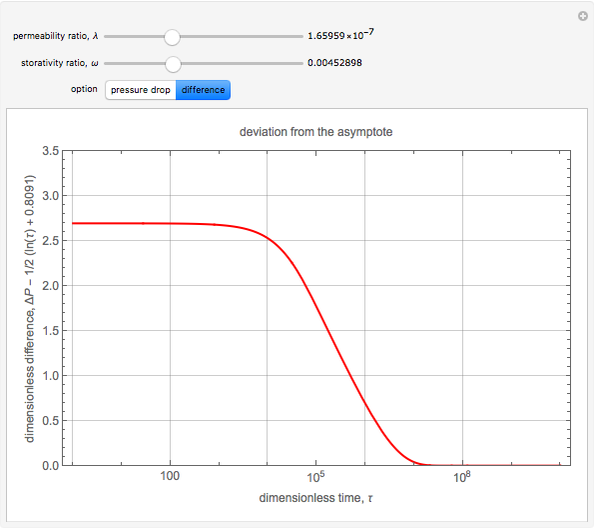
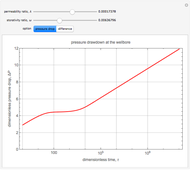
This Demonstration shows how the drawdown pressure in the well of an infinite (dual porosity), naturally fractured reservoir depends on the characteristics of the fractures and the surrounding matrix.
Contributed by: Landon Haynes (July 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In naturally fractured reservoirs, we use a model called dual porosity to account for the fractures in a matrix of porous material. The governing equations for a dual-porosity reservoir are the differential equations (written in dimensionless form):

and
 ,
,
where  is the (dimensionless) pressure in the fractures;
is the (dimensionless) pressure in the fractures; 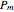 is the (dimensionless) pressure in the surrounding matrix;
is the (dimensionless) pressure in the surrounding matrix;  is a dimensionless parameter equal to the ratio of the fracture storativity to the total (fractures and matrix) storativity, where the storativity is the product of the compressibility and the porosity;
is a dimensionless parameter equal to the ratio of the fracture storativity to the total (fractures and matrix) storativity, where the storativity is the product of the compressibility and the porosity; 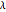 is a dimensionless parameter that is proportional to the ratio of the matrix permeability to the fracture permeability;
is a dimensionless parameter that is proportional to the ratio of the matrix permeability to the fracture permeability;  is the dimensionless radial distance from the wellbore; and
is the dimensionless radial distance from the wellbore; and  is the dimensionless time.
is the dimensionless time.
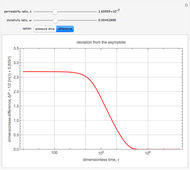
In 1963, Warren and Root [1] solved these equations for an infinite reservoir with uniform initial pressure that is produced by a constant flow rate, using Laplace transforms. The solution they found was that if 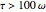 , then the drawdown pressure in the well is
, then the drawdown pressure in the well is
 ,
,
where 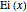 is the exponential integral.
is the exponential integral.
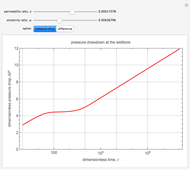
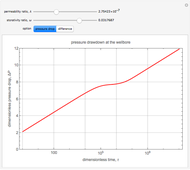
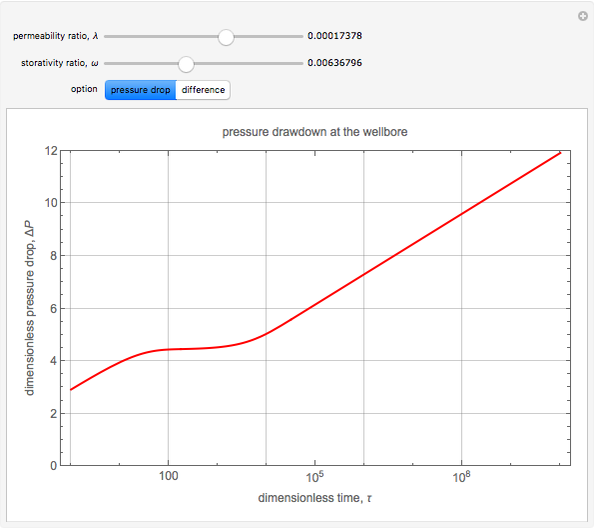
At early times, the oil flows into the well only through the fractures, as not enough time has passed for the oil to have flowed out of the surrounding matrix, because of the relatively low permeability compared to that of the fractures. Hence, in the early time regime, the reservoir acts as a single-porosity system depending only on the details of the fractures. For large time, enough time has passed for the oil to have flowed out of the voids of the matrix and into the fractures. Hence, in the large time limit, the reservoir acts as a single-porosity system whose permeability is dominated by the fractures (just like the early time limit), but the storativity now includes the effects of the fractures and the matrix.
There is a transition zone where the drawdown pressure in the well is essentially constant. During this transition, the flow into the well from the fractures matches the flow from the matrix into the fractures, and hence the drawdown pressure in the well is constant.
Reference
[1] J. E. Warren and P. J. Root, "The Behavior of Naturally Fractured Reservoirs," Society of Petroleum Engineers Journal, 3(3), 1963 pp. 245–255. doi:10.2118/426-PA.
Permanent Citation