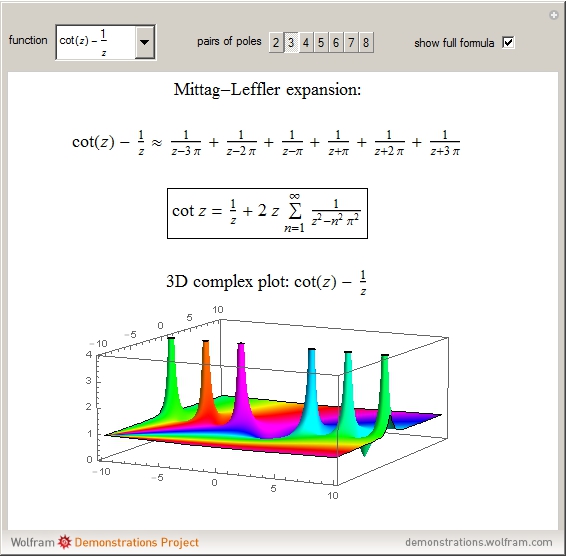
Mittag-Leffler Expansions of Meromorphic Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider a meromorphic function 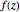 whose only singularities are simple poles at
whose only singularities are simple poles at 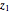 ,
, 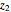 ,
,  , … (
, … (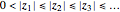 ) with residues
) with residues 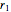 ,
,  ,
,  , … at these poles. Then
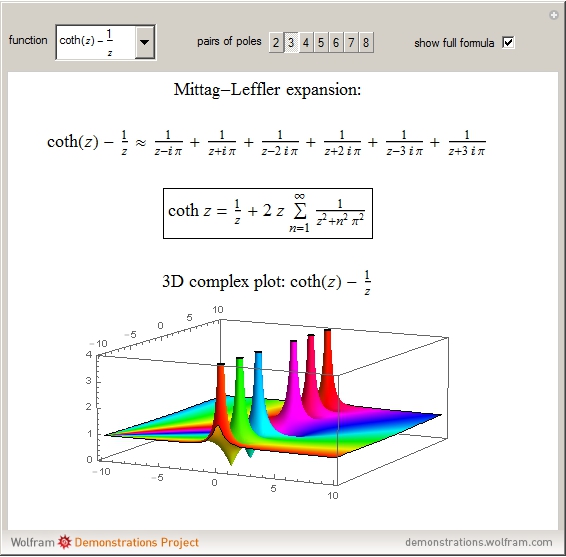
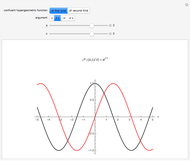
, … at these poles. Then 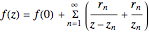 , a result known as the Mittag-Leffler (M-L) expansion [1, 2]. This Demonstration considers M-L expansions for the gamma function and several trigonometric functions with poles in the complex plane. You can construct explicit approximations for up to eight pairs of positive and negative poles and then display the full formula as
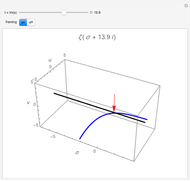
, a result known as the Mittag-Leffler (M-L) expansion [1, 2]. This Demonstration considers M-L expansions for the gamma function and several trigonometric functions with poles in the complex plane. You can construct explicit approximations for up to eight pairs of positive and negative poles and then display the full formula as  . A 3D plot of the function on the complex plane is also shown, with the poles appearing as spikes; the argument of the complex function is color-coded.
. A 3D plot of the function on the complex plane is also shown, with the poles appearing as spikes; the argument of the complex function is color-coded.
Contributed by: S. M. Blinder (April 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
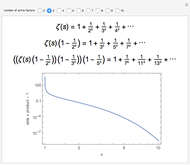
An early motivation for expansions using partial fractions was a result derived by Euler in Introductio in analysin infinitorum (1748):
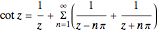 .
.
The M-L expansion has proven to be extremely useful in many applications to mathematical physics. The author's derivation for a closed form for the Coulomb propagator [3] was based on an M-L expansion of Green's function.
References
[1] E. T. Whittaker and G. N. Watson, A Course of Modern Analysis, 4th ed., London: Cambridge University Press, 1958 pp. 134ff.
[2] G. Mittag-Leffler, "En metod att analytisk framställa en funktion at rationel karacte...," Öfversigt Kongl. Vetenskaps-Akademiens Förhandlinger, 33, 1876 pp. 3–16.
[3] S. M. Blinder, "Analytic Form for the Nonrelativistic Coulomb Propagator," Physical Review A, 43(1), 1991 pp. 13–16. doi:10.1103/PhysRevA.43.13.
Permanent Citation