Absorption Spectroscopy

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
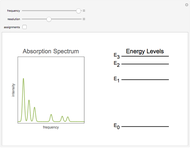
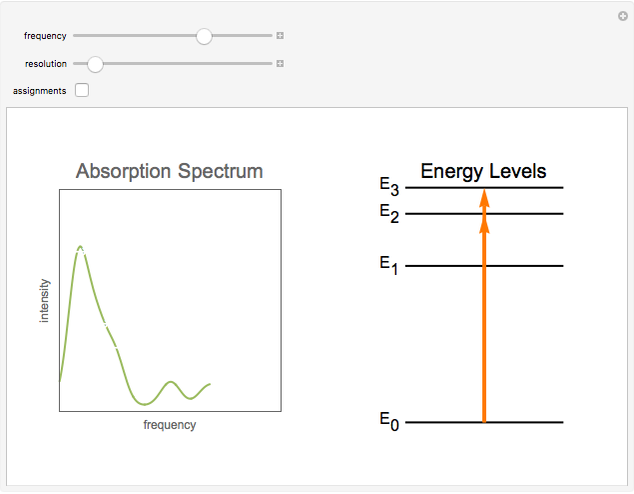
This Demonstration shows some general qualitative features of absorption spectroscopy, common to all types of spectroscopy. Given a stack of quantized energy levels—atomic, molecular or nuclear—radiation will be absorbed when its frequency  matches one of the energy level differences, according to the Bohr condition
matches one of the energy level differences, according to the Bohr condition 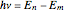 , assuming the transition is allowed by the appropriate selection rules.
, assuming the transition is allowed by the appropriate selection rules.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: The complete spectrum, after frequency sweeps over its full range.
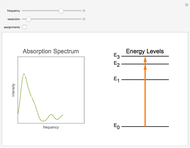
Snapshot 2: Assignments of the peaks are shown.
Snapshot 3: Spectrum at low resolution. The peaks become "washed out". An infrared spectrum like this one can still be useful to identify different compounds.
For more information, see S. M. Blinder, Introduction to Quantum Mechanics,pp 8-10.
Permanent Citation
"Absorption Spectroscopy"
http://demonstrations.wolfram.com/AbsorptionSpectroscopy/
Wolfram Demonstrations Project
Published: March 7 2011