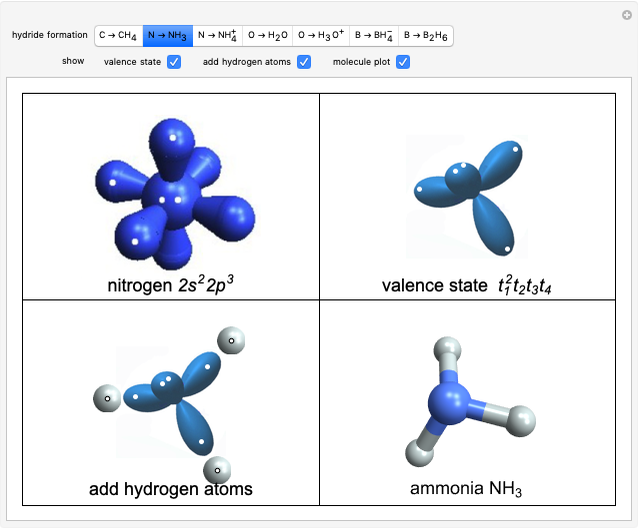
Statistical Thermodynamics of Ideal Gases

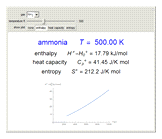
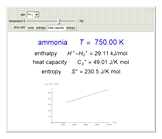
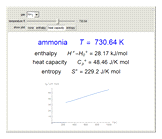
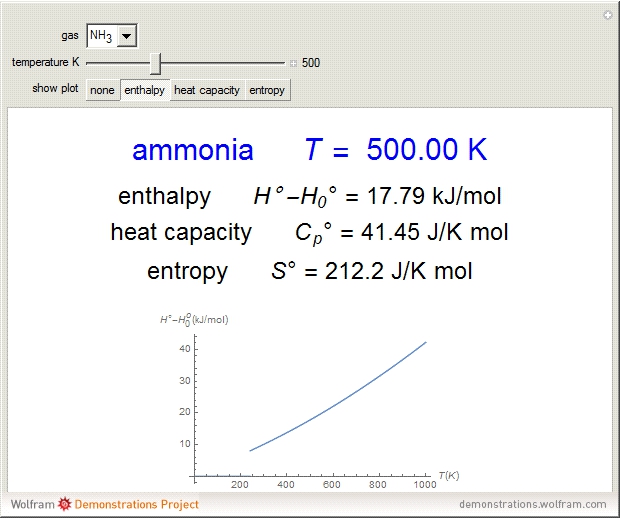
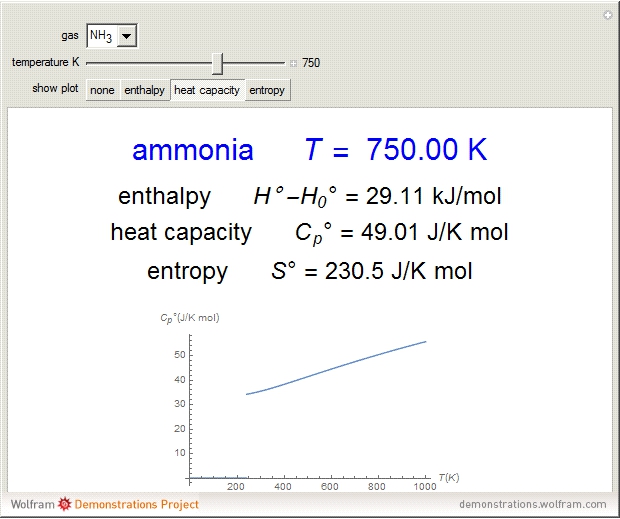
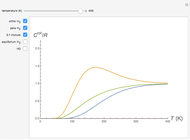
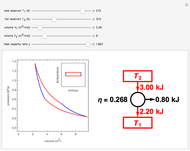
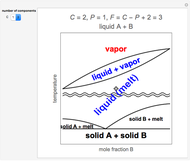
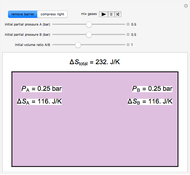
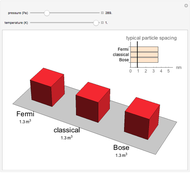
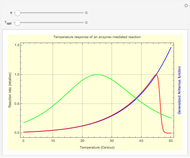
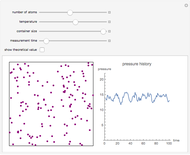
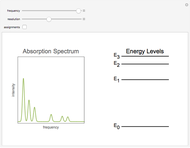
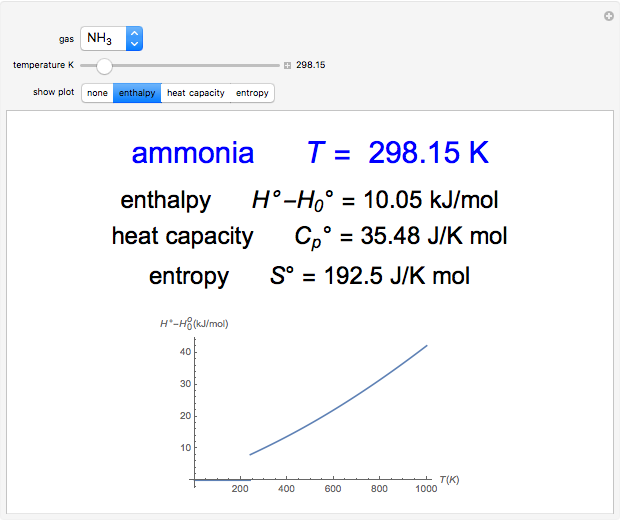
Thermodynamic properties of ideal gases, well approximated by real gases at a pressure of 1 atm, can be computed from molecular and spectroscopic parameters by the methods of statistical mechanics. For monatomic gases, only the molecular weights are needed. For polyatomic molecules, the fundamental vibrational frequencies and rotational constants , and , usually expressed in wavenumbers (), are also required. The rotational symmetry number is also needed, as well as the electronic degeneracy for the few molecules with non-singlet electronic ground states, such as and NO.

In this Demonstration, standard molar enthalpies, heat capacities, and entropies for 20 common gas molecules are computed by the methods of statistical thermodynamics. The temperature of each gas can be varied from its boiling temperature to 1000K. The calculated thermodynamic functions are accurate to within 0.1 and 0.5% of the corresponding experimental values. The molecuar weight should rigorously refer to a specific isotopic species but little error is made by using the chemical value . You can also show plots of these thermodynamic functions over the temperature range from the boiling point to 1000K.