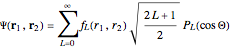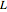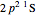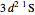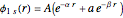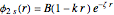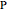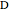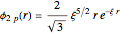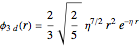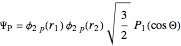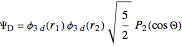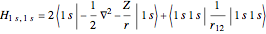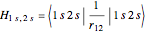Configuration Interaction for the Helium Isoelectronic Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
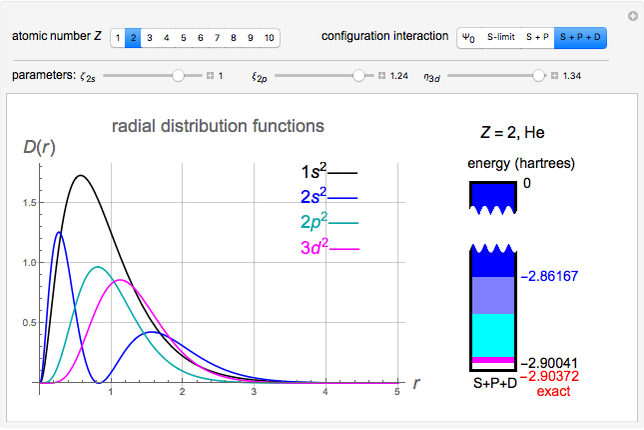
Configuration interaction (CI) provides a systematic method for improving on single-configuration Hartree–Fock (HF) computations [1, 2]. This Demonstration considers the two-electron atoms in the helium isoelectronic series. The HF wavefunction  is the optimal product of one-electron orbitals
is the optimal product of one-electron orbitals 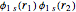 approximating the
approximating the  ground-state configuration. An improved representation of the ground state can be obtained by a superposition containing excited
ground-state configuration. An improved representation of the ground state can be obtained by a superposition containing excited  electronic configurations, including
electronic configurations, including 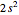 ,
, 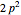 ,
,  , …, with relative contributions determined by the variational principle.
, …, with relative contributions determined by the variational principle.
Contributed by: S. M. Blinder (February 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
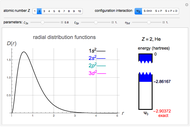
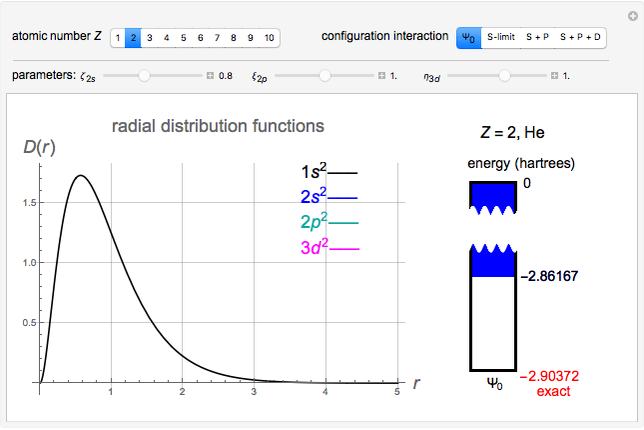
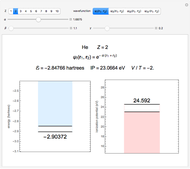
Snapshot 1: the single-configuration Hartree–Fock result
Snapshot 2: approximation to the  -limit; a more accurate computation gives
-limit; a more accurate computation gives  hartrees
hartrees
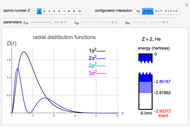
Snapshot 3: result using optimized parameters; reaching 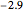 is considered a milestone
is considered a milestone
References
[1] S. M. Blinder, "The Hartree–Fock Approximation," Mathematical Physics in Theoretical Chemistry (S. M. Blinder and J. E. House, eds.), Amsterdam: Elsevier, forthcoming.
[2] Wikipedia. "Configuration Interaction." (Feb 14, 2018) en.wikipedia.org/wiki/Configuration_interaction.
[3] H. Shull and P.-O. Löwdin, "Superposition of Configurations and Natural Spin Orbitals: Applications to the He Problem," Journal of Chemical Physics, 30(3), 1959 pp. 617–626. doi:10.1063/1.1730019.
Permanent Citation