Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Equality of a Segment and an Arc in Archimedes's Spiral

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

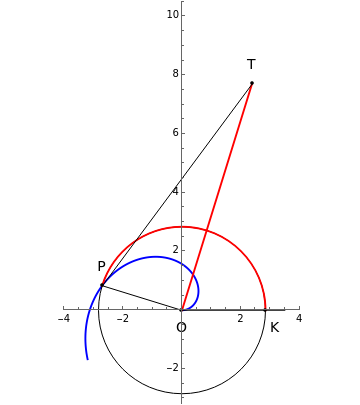
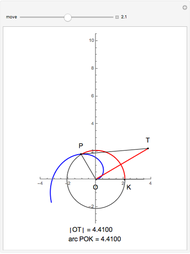
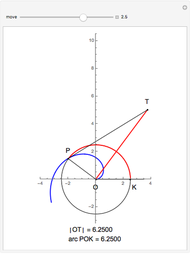
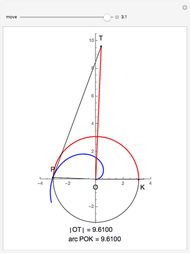
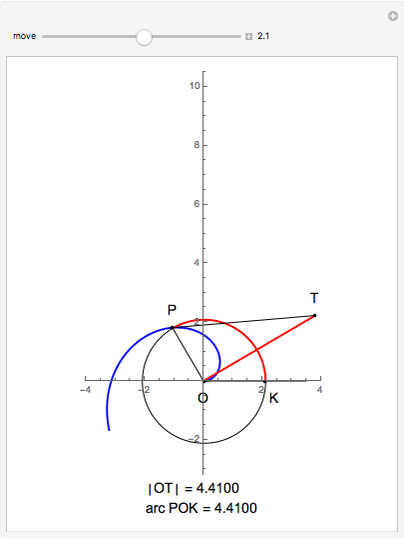
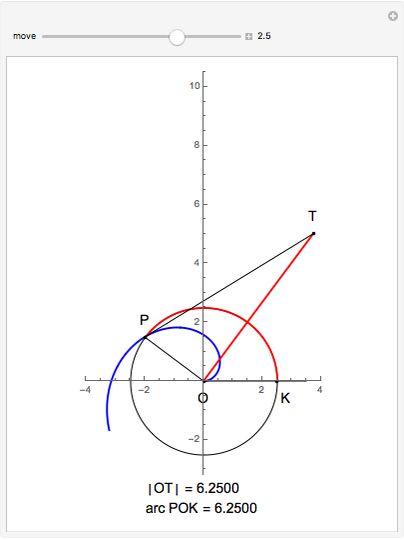
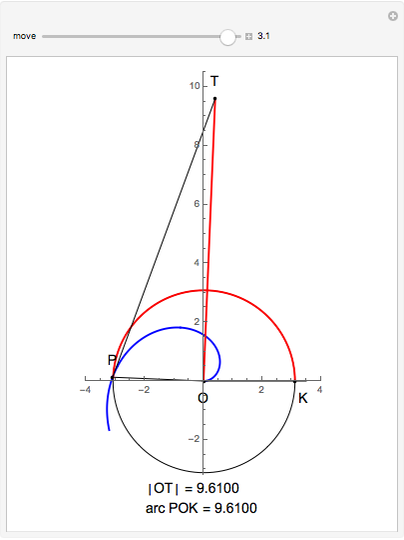
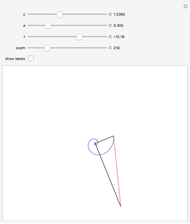
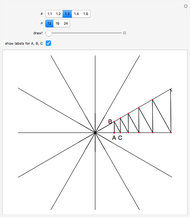
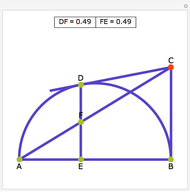
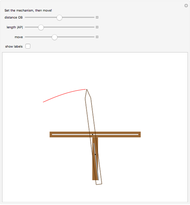
This Demonstration illustrates Proposition 20 of Archimedes's work On Spirals.

[more]

Let be any point on the first turn of the spiral, and let be the intersection of the tangent to the spiral at , with the perpendicular to at . Then .

[less]

Contributed by: Izidor Hafner (November 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] T. L. Heath (ed.), The Works of Archimedes, New York: Dover Publications, 2002.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send